必要な用語や手法に関する解説も一緒におこなっていきますので、参考書代わりに本記事を使ってみてください。
目次
令和４年測量士補試験No.１３の問題文
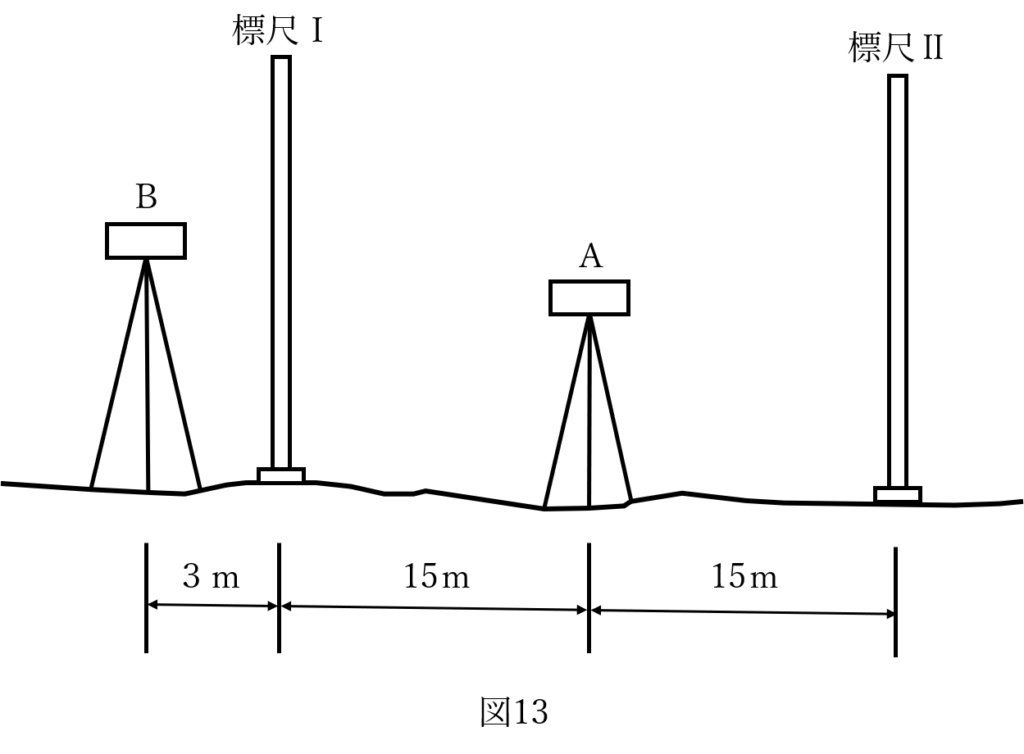
レベルの視準線を点検するために，図 13 のように A 及び B の位置で観測を行い，表 13 に示す結果を得た。この結果からレベルの視準線を調整するとき，B の位置において標尺Ⅱの読定値を幾らに調整すればよいか。最も近いものを次の中から選べ。
なお，関数の値が必要な場合は，巻末の関数表を使用すること。
- 1.5579 m
- 1.6250 m
- 1.7002 m
- 1.7021 m
- 1.7044 m
（令和4年測量士補試験問題集 No１３）
令和４年測量士補試験No.１３の解答・解説
「水準測量」の分野からの出題です。
解答は「３」となります。以下、詳しい計算手順の解説です。
B の位置において標尺Ⅱの読定値を幾らに調整すればよいかを計算する手順
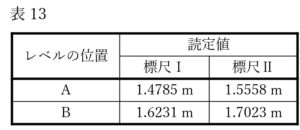
本問では「レベルを調整するにあたり、Bの位置にレベルを置いたときに標尺Ⅱのどの数値を読むように視準線を調整するべきか」を聞いています。
上記の値を求めるためには、以下の手順を踏む必要があります。
- レベルをAの位置に据えたときの標尺Ⅰと標尺Ⅱの位置の高低差を求める
- レベルをBの位置に据えたときの標尺Ⅰと標尺Ⅱの位置関係で作図する
- レベルをBの位置に据えたときの標尺Ⅰと標尺Ⅱの高低差の計算を利用して誤差ｘを求める
- 標尺Ⅱの正しい値を求める
それぞれの手順を詳しく見て見いきましょう！
手順１ レベルをAの位置に据えたときの標尺Ⅰと標尺Ⅱの位置の高低差を求める
まずは、レベルをAの位置に据えたときの、標尺Ⅰと標尺Ⅱの位置の高低差を求めていきます。
レベルをAの位置に据えたとき、
- Aの位置と標尺Ⅰの位置で15m
- Aの位置と標尺Ⅱの位置で15m
となっていて、レベルからそれぞれの標尺の距離は同じになっています。
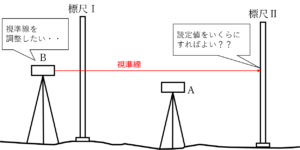
視準線は値を読む地点まではまっすぐに伸びるので、距離が同じであれば標尺Ⅰでも標尺ⅡでもAから読んだ値は同じだけ誤差を持つということになります。
仮にこの15m先での誤差の大きさをXとすると、次のように表すことができます。
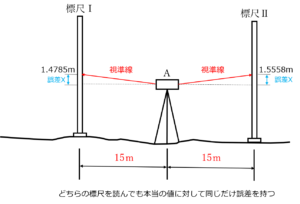ここで、標尺Ⅰと標尺Ⅱの高低差を出すにはAの位置からレベルで読んだ値を使って引き算すればよいのですが、どちらも同じ誤差Xを持っています。
よって、標尺Ⅰと標尺Ⅱの高低差は以下のように計算できます。
標尺Ⅰの地点と標尺Ⅱの地点の高低差
＝（標尺Ⅰの読定値＋誤差X）－（標尺Ⅱの読定値＋誤差X）
＝（1.4785m＋誤差X）－（1.5558m＋誤差X）
＝1.4785m－1.5558m＋誤差X－誤差X
＝－0.0773m
以上のことから、標尺Ⅰの地点と標尺Ⅱの地点の高低差＝－0.0773mと計算出来ました。
計算の中で誤差が打ち消されているため、上記計算結果は標尺Ⅰの地点と標尺Ⅱの地点の正しい高低差の値であることがわかります。
また、お気づきのかたもいるかもしれませんが「レベルを据えた位置から等距離にある標尺の高低差は正しい値になる」ことをわかっていれば、
標尺Ⅰの地点と標尺Ⅱの地点の高低差
＝（標尺Ⅰの読定値）－（標尺Ⅱの読定値）
＝1.4785m－1.5558m
＝－0.0773m
と算出することも可能です。
手順２ レベルをBの位置に据えたときの標尺Ⅰと標尺Ⅱの位置関係で作図する
この手順では、正しい視準線（水平な視準線）と傾いた視準線を利用して、以下のように作図をします。
また、地点Bから標尺Ⅱの正しい読定値をｅ（本問で求めたい値）としておきます。
ここで1mごとに誤差ｘが蓄積していくとすると、3m離れた標尺Ⅰの地点で3ｘ、33m離れた標尺Ⅱの地点33ｘの誤差がそれぞれ発生すると言えます。
手順３ レベルをBの位置に据えたときの標尺Ⅰと標尺Ⅱの高低差の計算を利用して誤差ｘを求める
表13にのっているB地点からレベルを用いて読んだ標尺Ⅰの値には3ｘ、標尺Ⅱの値には33ｘがそれぞれ含まれていると言えます。
よって、Ｂ地点から標尺Ⅰと標尺Ⅱの値は、含まれた誤差を差し引けば正しい値になるということです。よって、以下の通りそれぞれ表すことができます。
- 標尺Ⅰの正しい値＝1.6231－3ｘ
- 標尺Ⅱの正しい値ｅ＝1.7023－33ｘ
手順１で、正しい標尺Ⅰと標尺Ⅱの高低差＝－0.0773と出ているので、上記の「Ｂ地点から見た標尺Ⅰと標尺Ⅱの正しい値の高低差」も－0.0773となるはずです。
よって、以下の式を作ることができます。
Ｂ地点から見た標尺Ⅰの正しい値－Ｂ地点から見た標尺Ⅱの正しい値＝正しい標尺Ⅰと標尺Ⅱの高低差
（1.6231－3ｘ）－（1.7023－33ｘ）＝－0.0773
1.6231－1.7023－3ｘ＋33ｘ＝－0.0773
－0.0792＋30ｘ＝－0.0773
30ｘ＝0.0019
ｘ＝0.0019/30
手順４ 標尺Ⅱの正しい値を求める
さきほど、標尺Ⅱの正しい値ｅ＝1.7023－33ｘとあらわしたので、手順３で求めたｘ＝0.0019/30を代入すると
標尺Ⅱの正しい値ｅ＝1.7023－33ｘ
＝1.7023－33×（0.0019/30）
＝1.7023－0.0019×1.1
＝1.7023－0.00209
＝1.70021
となります。
よって、「レベルの視準線を調整するとき，B の位置において標尺Ⅱの読定値を1.70021 ｍに調整すればよい」となります。
よって正しい選択肢は「３」となります。
令和４年測量士補試験No.１３のまとめ
「水準測量」からの出題でした。
レベルの調整の問題は、頻出ではありませんがたまに出題される問題です。
忘れたころに出題されることも多いため、一度解答を導くための手順がしっかり確認しておくべきかと思います。
その他の測量士補試験の問題に挑戦！
令和4年のNO.13の問題を確認したら、その他の問題にも挑戦していきましょう！
本ブログでは各問題の解説を年度ごとに一覧にまとめたページがありますので、ぜひその記事からその他の問題に挑戦してみてください！
問題解説のまとめ記事はコチラからどうぞ！→過去問に挑戦！現役測量士の解説を読んで測量士補試験を攻略しよう！
さいごに
本ブログを参考にしていただきありがとうございます。
内容に関して不明な点、ご質問、指摘事項、感想などございましたら、コメントやメールにてご連絡ください。
励みになるとともに、本ブログをよりたくさんの皆様に有益なものにできると考えています。
ぜひお待ちしております。
お問い合わせ先：surveyor_kenzo☆aol.com
※ご連絡の際は☆を@に変更してください。