必要な用語や手法に関する解説も一緒におこなっていきますので、参考書代わりに本記事を使ってみてください。
目次
令和3年測量士補試験No.12の問題文
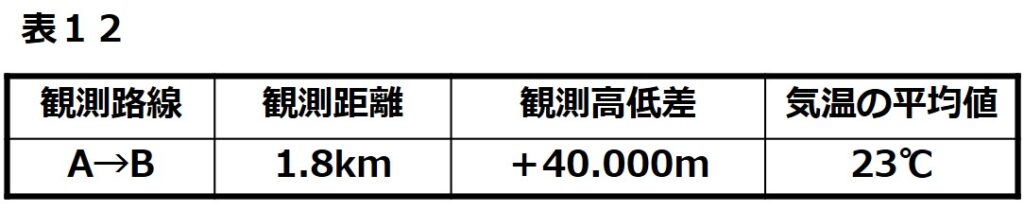
公共測量により,水準点 A,B の間で1級水準測量を実施し,表 12 に示す結果を得た。温度変化による標尺の伸縮の影響を考慮し,使用する標尺に対して標尺補正を行った後の,水準点A,B 間の観測高低差は幾らか。最も近いものを次の中から選べ。
ただし,観測に使用した標尺の標尺改正数は,20 ℃ において 1 m 当たり −8.0 × 10(−6乗) m,膨張係数は +1.0 × 10(−6乗) / ℃ とする。
なお,関数の値が必要な場合は,巻末の関数表を使用すること。(回答群)
1.+39.9991 m
2.+39.9996 m
3.+39.9998 m
4.+40.0000 m
5.+40.0004 m(令和3年測量士補試験問題集 No12より)
※使用する文字の関係で一部過去問の原本と表記が変わっている部分があります。
令和3年測量士補試験No.12の解答・解説
「水準測量」の分野からの出題です。
解答は「3」となります。以下、詳しい計算手順の解説です。
計算に使用する関数表はコチラを参考にしてください。→関数表
標尺補正後の観測高低差の考え方
本問題は、縮尺補正計算の問題です
使用する標尺に対して標尺補正を行った後の水準点A,B 間の観測高低差を求めたいので、標尺補正をするための標尺補正量を求める必要があります。
標尺補正数を求めたあとに、表12で示されている成果にその求めた補正量を適用してあげれば、求めたい解答を得ることができるということですね。
よって、解答を求めるためには次の手順を踏んでいく必要があります。
- 問題文から各数値が公式のどの文字に当てはまるのか考える
- 縮尺補正計算の公式に数値を当てはめて計算する
- 縮尺補正量を観測成果に適用する
それぞれの手順について、詳しく見ていきましょう!
標尺補正計算の公式
標尺補正量は以下の公式で求めることができます。
標尺補正計算の公式
ΔC={C0 +(T - T0)× α}× ΔH
ΔC:標尺補正量
C0:基準温度における標尺改正数(単位長さ当たりの補正量)
T:観測時の測定温度(℃単位)
T0:基準温度(℃単位)
α:膨張係数
ΔH:観測高低差(m単位)
また、この公式は国土地理院で定めている作業規程の準則(付録6計算式集)にも載っています。→作業規程の準則(付録6 計算式集)(P32)
あとはこの公式にそれぞれの数値を問題文から引用して当てはめていくだけです!
手順1 問題文から各数値が公式のどの文字に当てはまるのか考える
前述していますが、標尺補正量ΔCを求めるために必要な値は次の通りです。
- C0:基準温度における標尺改正数(単位長さ当たりの補正量)
- T:観測時の測定温度(℃単位)
- T0:基準温度(℃単位)
- α:膨張係数
- ΔH:観測高低差(m単位)
問題文からそれぞれの数値を読み解くと、次のようになります。
- C0:基準温度における標尺改正数(単位長さ当たりの補正量)→−8.0 × 10(−6乗)m (問題文2段落目より)
- T:観測時の測定温度(℃単位)→23℃(表12より)
- T0:基準温度(℃単位)→20℃(問題文2段落目より)
- α:膨張係数→+1.0 × 10(−6乗) / ℃(問題文2段落目より)
- ΔH:観測高低差(m単位)→40.000m(表12より)
手順2 縮尺補正計算の公式に数値を当てはめて計算する
前章で考えた各数値を公式(ΔC={C0 +(T - T0)× α}× ΔH)に当てはめると、次のような計算になりますね。
ΔC={−8.0 × 10(−6乗)m +(23℃ - 20℃)× 1.0 × 10(−6乗) / ℃ } × 40.000m
まずは()の中から計算して
ΔC={-8.0 × 10-(-6乗)m + 3℃ × 1.0 × 10(−6乗) / ℃ } × 40.000m
続いて{}の中の掛け算だけ計算して
ΔC={-8.0 × 10(-6乗)m + 3.0 × 10(−6乗)} × 40.000m
次に{}の中の足し算をして
ΔC={-5.0 × 10(-6乗)}× 40.000m
最後に残った数値を掛け算して
ΔC=-0.0002m
よって、-0.0002mが求めたい縮尺補正量となります。
手順3 縮尺補正量を観測成果に適用する
23℃のときの縮尺補正量を求めることができたので、観測成果に適用します。
今回は表12から観測高低差が40.000mと出ているので、縮尺補正量ΔC=-0.0002を足してあげれば回答が出ます。
ここで1つ注意が必要なのが「観測高低差-符号がついている場合でも計算する際は絶対値で考える」ということです。
例えば観測高低差が-40.000mであった場合でも、計算する際は40.000mと捉えて計算する必要があるということですね。
今回は観測高低差が40.000mなのでそこまで気にする必要はないですが、出題内容によっては注意が必要になってきます。
それでは計算に戻りますが、求める計算は次のようになります。
使用する標尺に対して標尺補正を行った後の水準点A,B 間の観測高低差=|40.000m|+(-0.0002m)
=39.9998m
※||は絶対値の記号
よって本問題の答えは39.9998である「3」が答えとなります。
令和3年測量士補試験No.12のまとめ
「水準測量」からの出題でした。
今回は、標尺補正計算に関する問題で、出題頻度は低くはありません。
公式の暗記や、標尺補正量を適用する際の観測高低差の符号の考え方など気しておくべき部分は多いので、ミスが出ないように類題もどんどん解いていきましょう!
令和3年測量士補試験No.12の類題
過去に出題された本問の類題です!ぜひチャレンジしてみてください!
令和2年測量士補試験問題集NO.13→問題文及び解説記事はコチラ
その他の測量士補試験の問題に挑戦!
令和3年のNO.12の問題を確認したら、その他の問題にも挑戦していきましょう!
本ブログでは各問題の解説を年度ごとに一覧にまとめたページがありますので、ぜひその記事からその他の問題に挑戦してみてください!
問題解説のまとめ記事はコチラからどうぞ!→過去問に挑戦!現役測量士の解説を読んで測量士補試験を攻略しよう!
さいごに
本ブログを参考にしていただきありがとうございます。
内容に関して不明な点、ご質問、指摘事項、感想などございましたら、コメントやメールにてご連絡ください。
励みになるとともに、本ブログをよりたくさんの皆様に有益なものにできると考えています。
ぜひお待ちしております。
お問い合わせ先:surveyor_kenzo☆aol.com
※ご連絡の際は☆を@に変更してください。