必要な用語や手法に関する解説も一緒におこなっていきますので、参考書代わりに本記事を使ってみてください。
目次
令和３年測量士補試験No.２７の問題文
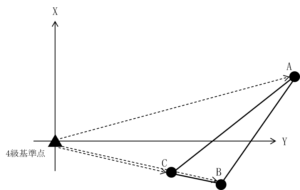
表 27 は，公共測量により設置された4級基準点から図 27 のように三角形の頂点に当たる地点A，B，C をトータルステーションにより測量した結果を示している。地点 A，B，C で囲まれた三角形の土地の面積は幾らか。最も近いものを次の中から選べ。
なお，関数の値が必要な場合は，巻末の関数表を使用すること。
- 55.904㎡
- 108.000㎡
- 138.440㎡
- 187.061㎡
- 200.000㎡
（令和3年測量士補試験問題集 No27）
令和３年測量士補試験No.２７の解答・解説
「応用測量」の分野からの出題です。
正解は「２」となります。
以下、詳しい計算手順の解説です。
計算に使用する関数表はコチラを参考にしてください。→関数表
地点A、B、Cで囲まれた三角形の土地の面積の求め方
地点A、B、Cで囲まれた三角形の土地の面積の求めるには、次のような手順を踏んでいきます。
- 問題文からわかる情報を図に書き込む
- 地点A、B、Cの座標を求める
- 座標法の面積計算で地点A、B、Cで囲まれた三角形の土地の面積を出す
それでは、1つ1つの手順を詳しく見ていきましょう。
手順１ 問題文からわかる情報を図に書き込む
まずは、問題文の表27に書いてある情報を図に書き込んでいきます。
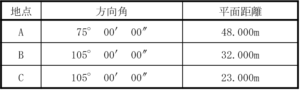方向角はX軸の上側を起点として右回りに進んだ時の角度を表しているので、平面距離と合わせて書くと下図のようになります。
この図を使用して、手順２を進めていきましょう！
手順２ 地点A、B、Cの座標を求める
手順２では、地点A、B、Cの各座標を求めていきます。
各地点と座標軸で構成される三角形がそれぞれあるのでsinやcosを使用して計算すればいいのですが、sinやcosに慣れていない人には少し難しい所です。
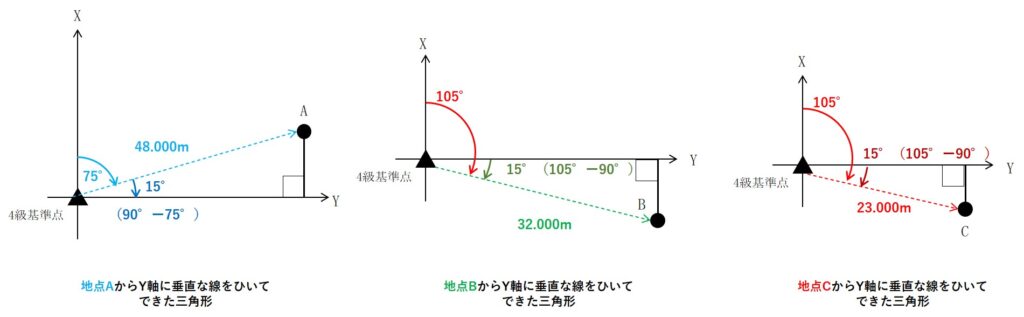
そこで下図のように各地点から横軸に向かって垂直な線を引いて各地点の三角形を作ってみると、sinやcosの使い方がわかりやすくなります。
どの直角三角形も斜めの辺と角度が分かっているので、sinとcosの関係を利用すると各地点のX座標とY座標を出すことができます。
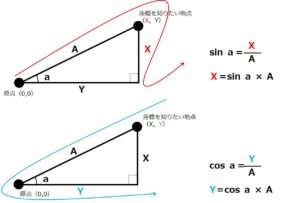
ちなみにsinとcosの計算の方法は下図のように形でイメージすると覚えやすいです。
上記手法で導き出した各地点の座標はsinとcosを用いると次のようにも表すことができます。
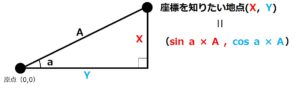よって各地点のそれぞれの座標は、次の計算で求めることが可能です。
地点Aについて
地点Bについて
地点Cについて
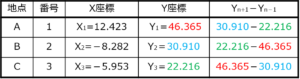
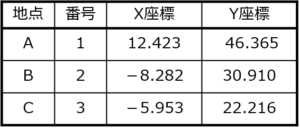
よって各地点の（X，Y）のそれぞれの座標は
- 地点A＝（12.423，46.365）
- 地点B＝（－8.282，30.910）
- 地点C＝（－5.953，22.216）
となります。地点Bと地点Cの位置はX軸の－側にいることに注意しましょう！
手順３ 座標法の面積計算で地点A、B、Cで囲まれた三角形の土地の面積を出す
各地点で囲まれた地形の面積を求めるには、座標法という面積計算の方法を使います。
面積計算を行うには各地点を時計回りに番号付けし、表にまとめる必要があります。
時計回りの出発点はどこでもいいので、本問では地点Aを1番として、時計回りに地点を2番、Cを3番にします。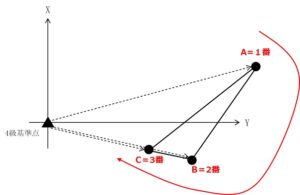
さらに上図の内容を表にまとめていきましょう。
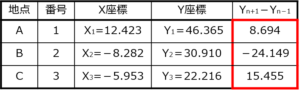
次に、各地点の「Y(n+1)－Y(n-1)」の値を出していきます。
例えば、地点Aの場合は「地点B（2番）のY座標の値」から「地点C（3番）のY座標の値」を引くことで「Y(n+1)－Y(n-1)」の値を求めることができます。
まとめると、以下の表のようになります。
計算すると以下のような感じですね。
上記の計算が終わったら、その計算結果に対してX座標をかけていきます。
計算すると以下のような結果になります。
ここまで来たら後は上記の計算結果を全て足して、それを2で割れば完了です。
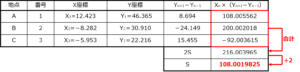よって、地点A、B、Cで囲まれた三角形の土地の面積は108.0019825≒108.002㎡と計算出来ました。
108.002㎡に最も近い値の選択肢は２ですので、正解は「２」となります。
令和３年測量士補試験No.２７のまとめ
応用測量の分野からの出題でした。
最後まで解いていただいた方は、長い道のりに感じかられたかと思います。
ただ、この座標法による面積計算は頻出なので測量士補試験にとっては必須の知識です！
今回の問いでは三角形の地形でしたが、四角形の場合もありますので様々なパターンに対応できるようにしていきましょう！
令和３年測量士補試験No.２７の類題
他年度の測量士補試験に出題された本問の類題です！ぜひチャレンジしてみてください！
令和2年測量士補試験問題集NO.27→問題文及び解説記事はコチラ
令和4年測量士補試験問題集NO.27→問題文及び解説記事はコチラ
その他の測量士補試験の問題に挑戦！
令和3年のNO.27の問題を確認したら、その他の問題にも挑戦していきましょう！
本ブログでは各問題の解説を年度ごとに一覧にまとめたページがありますので、ぜひその記事からその他の問題に挑戦してみてください！
問題解説のまとめ記事はコチラからどうぞ！→過去問に挑戦！現役測量士の解説を読んで測量士補試験を攻略しよう！
さいごに
本ブログを参考にしていただきありがとうございます。
内容に関して不明な点、ご質問、指摘事項、感想などございましたら、コメントやメールにてご連絡ください。
励みになるとともに、本ブログをよりたくさんの皆様に有益なものにできると考えています。
ぜひお待ちしております。
お問い合わせ先：surveyor_kenzo☆aol.com
※ご連絡の際は☆を@に変更してください。