必要な用語や手法に関する解説も一緒におこなっていきますので、参考書代わりに本記事を使ってみてください。
目次
令和3年測量士補試験No.26の問題文
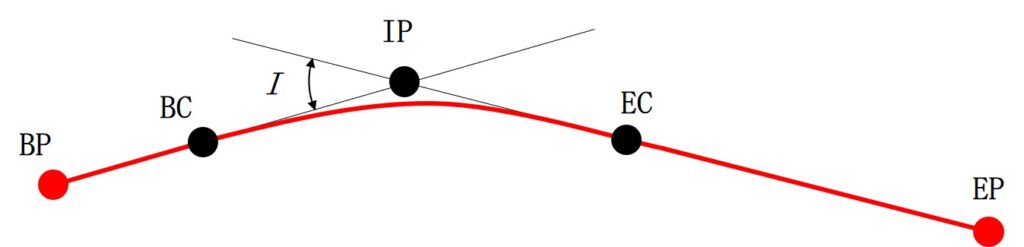
次の図 26 に示すように,始点 BC,終点 EC,曲率半径 R = 1,000 m,交角 I = 36 ° の円曲線(BC 〜 EC),直線(BP 〜 BC)及び直線(EC 〜 EP)を組み合わせた道路を建設したい。
BP から BC までの距離は 215 m,EC から EP までの距離は 500 m としたとき,BP から EPまでの距離は幾らか。最も近いものを次の中から選べ。
なお,円周率 π = 3.14とし,関数の値が必要な場合は,巻末の関数表を使用すること。
- 1.029m
- 1.128m
- 1.238m
- 1.343m
- 1.558m
(令和3年測量士補試験問題集 No26)
令和3年測量士補試験No.26の解答・解説
「応用測量」の分野からの出題です。
正解は「4」となります。
以下、詳しい計算手順の解説です。
計算に使用する関数表はコチラを参考にしてください。→関数表
BP~EPの長さを求めるまでの考え方
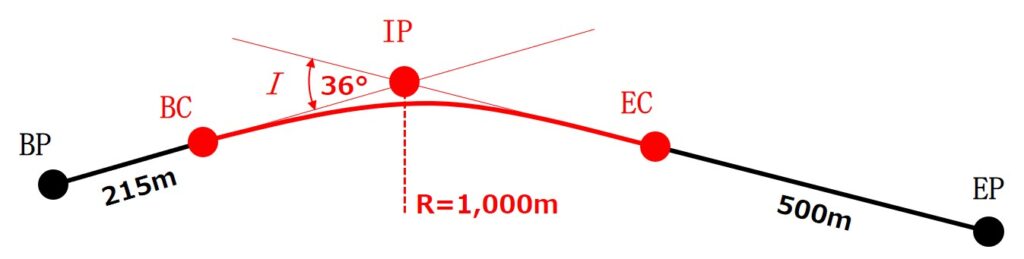
まず、図26の中のBP~EPというのは下図で着色している道路です。
問題文にもあるようにこの道路は
- 円曲線BC~EC
- 直線BP~BC
- 直線EC~EP
の3つの道路が組み合わさってできています。
 つまり「BP~BCの直線道路+BC~ECの円曲線道路+EC~EPの直線道路」でBP~EPの道路の長さが出るということです。
つまり「BP~BCの直線道路+BC~ECの円曲線道路+EC~EPの直線道路」でBP~EPの道路の長さが出るということです。
よって回答を導く手順としては
- 問題文から読み取れる情報を図に整理する
- BC~ECの円曲線道路の長さを求める
- BP~BC、BC~EC、EC~EPをそれぞれたす
で求めることができます。
それでは実際に手順ごとに内容を見てみましょう!
手順1 問題文から読み取れる情報を図に整理する
まずは、問題文から読み取れる情報を図に整理してみます。
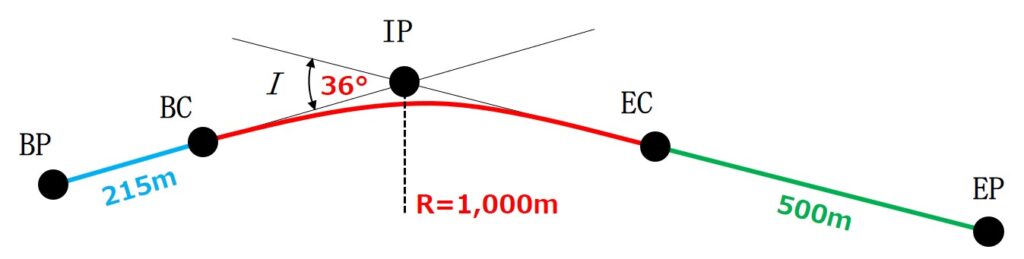
まず、円曲線BC~ECに関して読み取れることは以下の通りです。
- 曲率半径R=1,000m
- 交角I=36°
また、直線道路BP~BCとEC~EPについては以下のことが分かっています。
- BP~BC=215m
- EC~EP=500m
上記のことを図に整理すると以下のようになります。
これで問題文の情報を図に整理できました!
次は円曲線BC~ECの長さを求めていきましょう!
手順2 BC~ECの円曲線道路の長さを求める
この手順では、円曲線BC~ECの長さを求めていきます。
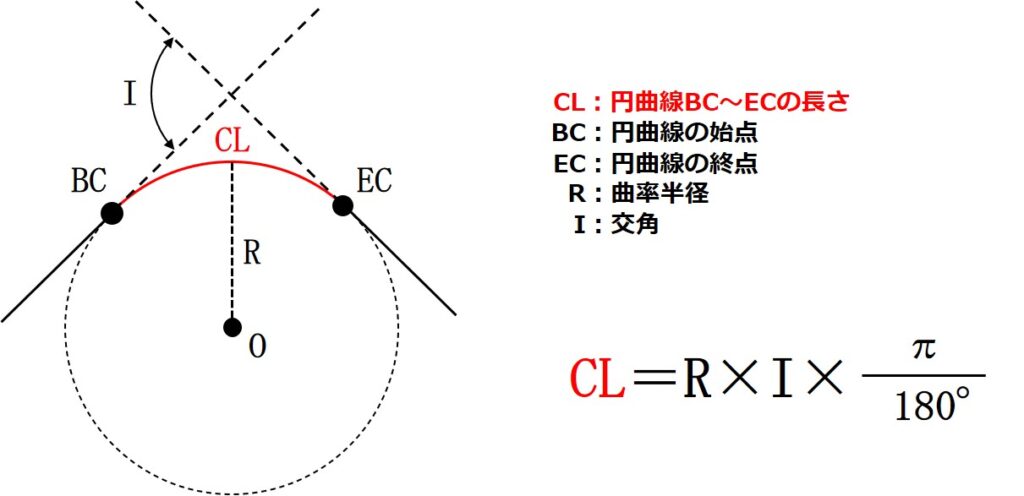
円曲線をもとめる一般的な公式は次の通りです。
この公式に図26の円曲線BC~ECの要素を当てはめると
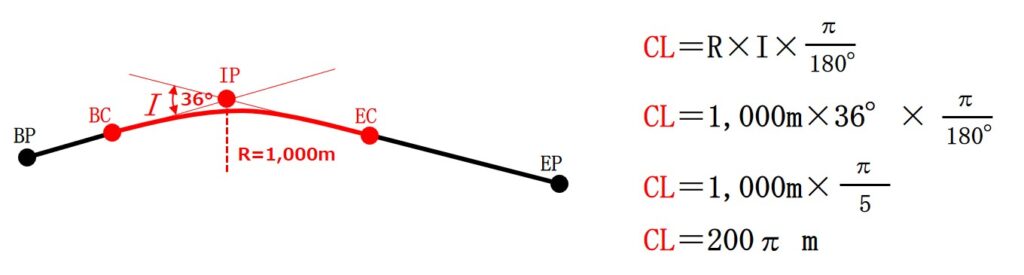 となります。CLはBC~ECのことなので、BC~EC=200π mになります。
となります。CLはBC~ECのことなので、BC~EC=200π mになります。
問題文でπ=3.14とすると述べていますので
BC~EC=200π=200×3.14≒628となります。
手順3 BP~BC、BC~EC、EC~EPをそれぞれたす
手順3ではBP~EPまでの長さを求めていきます。
BP~EPは
- 直線BP~BC
- 円曲線BC~EC
- 直線EC~EP
の3つの道路で構成されているので、上記3つの道路をすべて足せば、BP~EPまでの長さが求まるわけです。
よってBP~EPを求める式と計算は
BP~EP=BP~BC+BC~EC+EC~EP
=215m+628m+500m
=1,343m
となります。
よってBP~EP=1,343mとなるので、選択肢4が正解となります。
令和3年測量士補試験No.26のまとめ
応用測量の分野からの出題でした。
応用測量のうち、円曲線を含んだ道路の延長を求める問題です。
この問題のポイントは円曲線の長さの計算となります。
攻略できるようにしっかりと公式を覚えておきましょう!
令和3年測量士補試験No.26の類題
他年度の測量士補試験に出題された本問の類題です!ぜひチャレンジしてみてください!
令和2年測量士補試験問題集NO.26→問題文及び解説記事はコチラ
令和4年測量士補試験問題集NO.25→問題文及び解説記事はコチラ
その他の測量士補試験の問題に挑戦!
令和3年のNO.26の問題を確認したら、その他の問題にも挑戦していきましょう!
本ブログでは各問題の解説を年度ごとに一覧にまとめたページがありますので、ぜひその記事からその他の問題に挑戦してみてください!
問題解説のまとめ記事はコチラからどうぞ!→過去問に挑戦!現役測量士の解説を読んで測量士補試験を攻略しよう!
さいごに
本ブログを参考にしていただきありがとうございます。
内容に関して不明な点、ご質問、指摘事項、感想などございましたら、コメントやメールにてご連絡ください。
励みになるとともに、本ブログをよりたくさんの皆様に有益なものにできると考えています。
ぜひお待ちしております。
お問い合わせ先:surveyor_kenzo☆aol.com
※ご連絡の際は☆を@に変更してください。

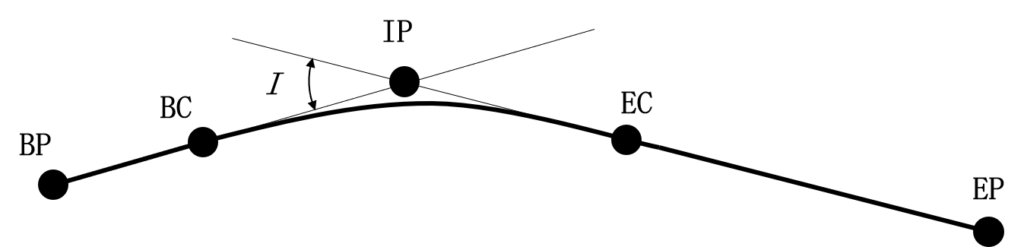 図26
図26