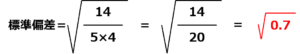必要な用語や手法に関する解説も一緒におこなっていきますので、参考書代わりに本記事を使ってみてください。
目次
令和４年測量士補試験No.３の問題文
次の文は，測量の誤差について述べたものである。（ア）～（エ）に入る語句及び数値の組合せとして最も適当なものはどれか。次の中から選べ。なお，関数の値が必要な場合は，巻末の関数表を使用すること。
（ア）は，測定の条件が変わらなければ大きさや現れ方が一定している誤差である。一方，（イ）は，原因が不明又は原因が分かってもその影響を除去できない誤差である。
このように測定値には誤差が含まれ，真の値を測定することは不可能である。
しかし，ある長さや角度に対する（イ）だけを含む測定値の一群を用いて，理論的に，真の値に最も近いと考えられる値を求めることは可能であり，このようにして求めた値を，最確値という。
ある水平角について，トータルステーションを用いて同じ条件で 5 回測定し，表 3 の結果を得たとき，（ア）が取り除かれているとすれば，最確値は（ウ），最確値の標準偏差の値は（エ）となる。
- （ア）系統誤差（イ）偶然誤差（ウ）45°22′23″（エ）0.8″
- （ア）系統誤差（イ）偶然誤差（ウ）45°22′25″（エ）0.8″
- （ア）系統誤差（イ）偶然誤差（ウ）45°22′25″（エ）1.7″
- （ア）偶然誤差（イ）系統誤差（ウ）45°22′23″（エ）1.7″
- （ア）偶然誤差（イ）系統誤差（ウ）45°22′25″（エ）1.7″
（令和4年測量士補試験問題集 No３）
令和４年測量士補試験No.３の解答・解説
「測量に関する法規」の分野からの出題になります。
解答は「２」となります。
以下、（ア）～（エ）についての詳しい解説です。
（ア）について
『（ア）は，測定の条件が変わらなければ大きさや現れ方が一定している誤差である。』
上記文章の（ア）には系統誤差が入ります。
例えば
- 温度による物体の伸縮
- 蜃気楼や陽炎のような空気のゆらぎ
- 器械そのもののクセ
などが当たりますね。
測定する際の手順であったり、決まりを守ることである程度対応が可能な誤差が系統誤差に当たります。
（イ）について
『（イ）は，原因が不明又は原因が分かってもその影響を除去できない誤差である。』
上記文章の（イ）には偶然誤差が入ります。
例えば
- 読み間違い
- 器械の設定ミス
- その他、なぜかわからないが起こる誤差
など誤差に対しての対応が難しくどうしても偶発的に発生してしまう誤差のことを偶然誤差と言います。
（ウ）について
（ウ）を考えるには、トータルステーションで水平角を同じ条件で５回測定したときの最確値を求める必要があります。
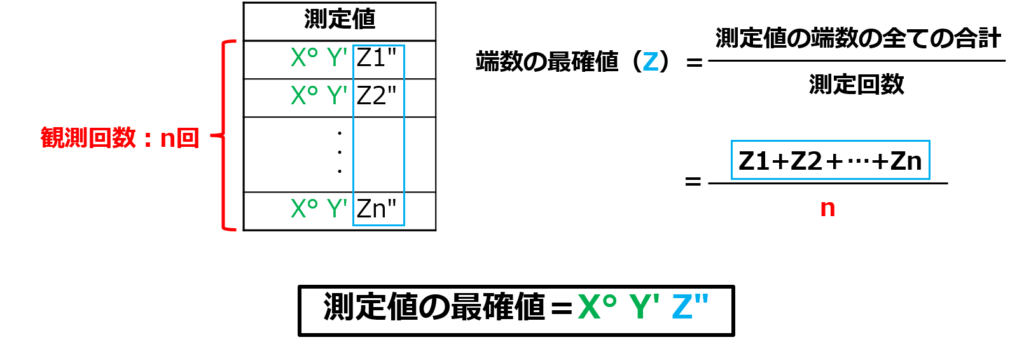
最確値を求めるには、以下のような考え方・計算方法を使います。
ここで改めて表を見てみると、
となっています。度と分の値は同じなので秒の値の最確値を出せばトータルステーションで水平角を5回測定したときの観測値の最確値を求めることができますね。
そこで、まずは秒の値の最確値を以下のように計算して求めていきます。
秒の値の最確値＝25″と出ましたので、あとはあたまに45°22′をつけるだけです。
よってトータルステーションで水平角を同じ条件で５回測定したときの最確値は45°22′25″となります。
（エ）について
（エ）を考えるには（ウ）で求めた最確値の標準偏差を求める必要があります。
標準偏差を求めるには
- それぞれの測定の最確値と測定値の差を求める
- 手順１で求めた数値をそれぞれ2乗する
- 手順２で求めた数値をすべて足す
- 標準偏差を求める公式に当てはめて計算する
の4つの手順を踏みます。
また、今回の測定では「45°22′」についてはすべて一定でしたので、秒の値についてのみ考えれば大丈夫です。
それでは、それぞれの手順について詳しく見ていきましょう！
手順１ それぞれの測定の最確値と測定値の差を求める
まずは、それぞれの測定の最確値と測定値の差を求めていきます。
差を求めるときには、下図のような表を作成すると求めやすいです。
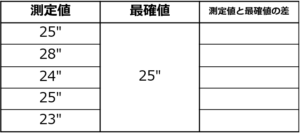あとは、この表を埋めるように測定値と最確値の差を計算していきます。
これでそれぞれの測定値と最確値の差を求めることができました！
ちなみにこの測定値と最確値の数値の差のことを残差と呼びます。
手順２ 手順１で求めた数値をそれぞれ2乗する
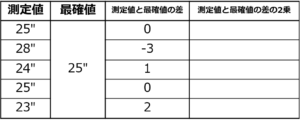
この手順では、手順１で求めた測定値と最確値の数値の差を2乗していきます。
手順１で使用した表に付け足すように以下の表を作ると求めやすいです。
あとはこの表を埋めるように計算していきます。
これで測定値と最確値の数値の差を2乗を求めることができました！
手順３ 手順２で求めた数値をすべて足す
この手順では、手順２で求めた数値をすべて足します。
手順２で使用した表にさらにもう一列、つけたしてあげるとまとめやすいです。
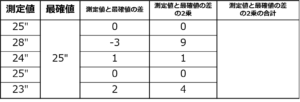あとはこの表を埋めるように、測定値と最確値の差の2乗の数値の合計を出してあげます。
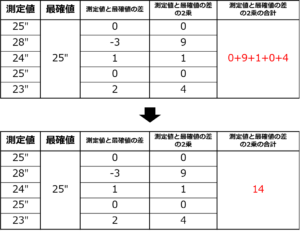これで測定値と最確値の差の2乗の数値の合計を求めることができました！
手順４ 標準偏差を求める公式に当てはめて計算する
まず、標準偏差を求める公式は次の通りです。
この公式に、手順３までで求めた定値と最確値の差の2乗の数値の合計の数値（14）と測定回数（5）を当てはめると、次のようになりますね。
ここで関数表を使用したいところですが、関数表の√の部分には、0.7が載っていないので数値がわからないので困りました…。
こういうときは、以下の関係性を使用します。
具体的には、
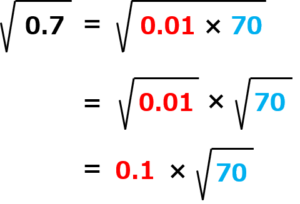のように√の中身を関数表の値に対応できるように分解してしまうということです。
今回であれば√の関数表には70の値が載っていますので0.7を0.07×70に分解して、√70の値に対して0.1をかければ標準偏差の値が出るように工夫しました。
ここで改めて関数表を参考にすると70のところには「8.36660」と載っています。
（手元に関数表がない方はコチラを参考にしてください→関数表）
あとはこの8.36660に0.1をかければ0.83666となります。
よって標準偏差＝0.83666≒0.8と出ました。
令和４年測量士補試験No.３のまとめ
「測量に関する法規」からの出題でした。
例年とは問題のタイプが変化し、用語と計算問題が混同されて出題されていました。
また、標準偏差の計算ではひと工夫必要となりますので、テクニックを覚える必要もあります。
少し難しい部分もあるかもしれませんが、標準偏差の計算は例年出ている頻出の計算なので、計算手順・方法だけはかならず覚えておきましょう！
手順を覚えるのが苦手な方は、本記事の表を作りながら計算すれば解きやすいのではないかと思います。
その他の測量士補試験の問題に挑戦！
令和4年のNO.3の問題を確認したら、その他の問題にも挑戦していきましょう！
本ブログでは各問題の解説を年度ごとに一覧にまとめたページがありますので、ぜひその記事からその他の問題に挑戦してみてください！
問題解説のまとめ記事はコチラからどうぞ！→過去問に挑戦！現役測量士の解説を読んで測量士補試験を攻略しよう！
さいごに
本ブログを参考にしていただきありがとうございます。
内容に関して不明な点、ご質問、指摘事項、感想などございましたら、コメントやメールにてご連絡ください。
励みになるとともに、本ブログをよりたくさんの皆様に有益なものにできると考えています。
ぜひお待ちしております。
お問い合わせ先：surveyor_kenzo☆aol.com
※ご連絡の際は☆を@に変更してください。