必要な用語や手法に関する解説も一緒におこなっていきますので、参考書代わりに本記事を使ってみてください。 その他の過去問の解説記事はコチラのリンクからどうぞ。
目次
令和2年測量士補試験No.26の問題文
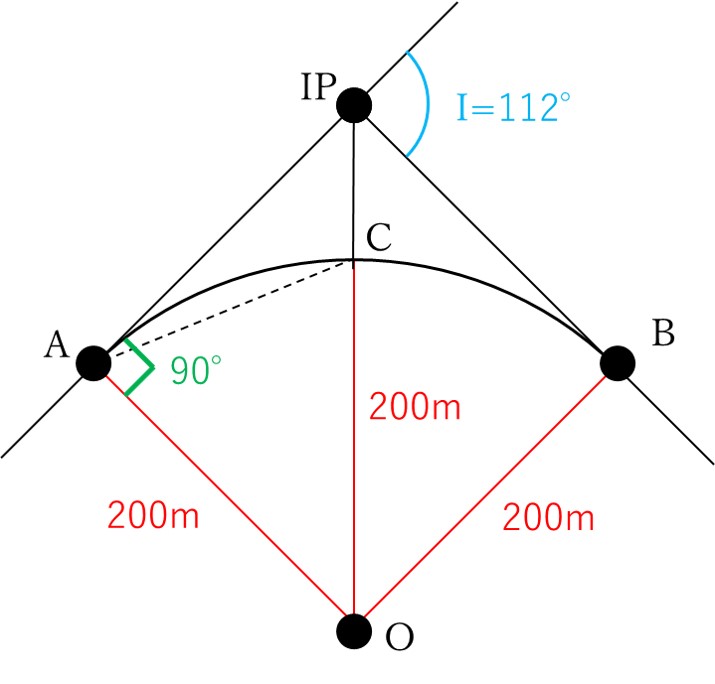
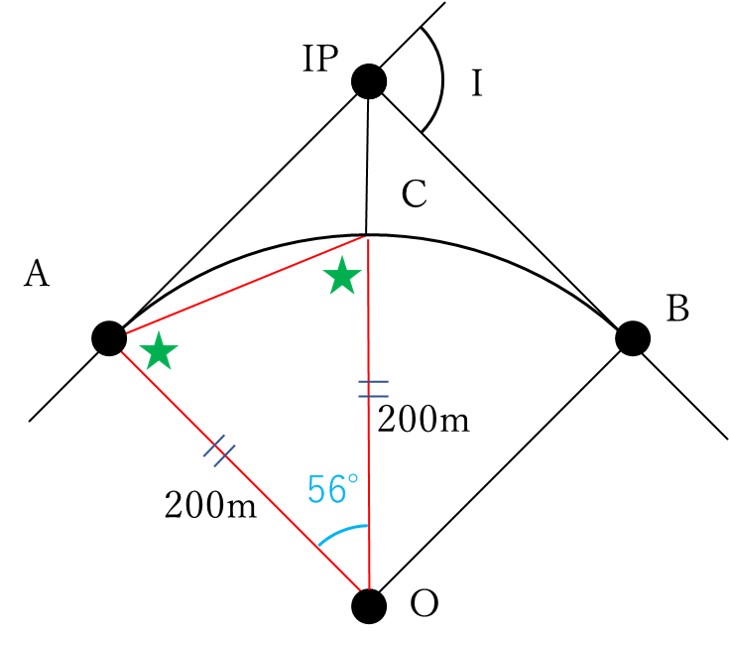
図26に示すように,点Aを始点,点Bを終点とする円曲線の道路の建設を計画している。曲線半径R =200 m,交角I =112°としたとき,建設する道路の点Aから円曲線の中点Cまでの弦長は幾らか。最も近いものを次の中から選べ。
なお,関数の値が必要な場合は,巻末の関数表を使用すること。
- 152 m
- 172 m
- 188 m
- 195 m
- 202 m
(令和2年測量士補試験問題集 No.26)
令和2年測量士補試験No.26の解答・解説
「応用測量」の分野からの出題です。
正解は「3」となります。
以下、解答を導くまでの詳しい計算の解説です。
計算に使用する関数表はコチラを参考にしてください。→関数表
道路の点Aから円曲線の中点Cまでの弦長を求めるまでの考え方
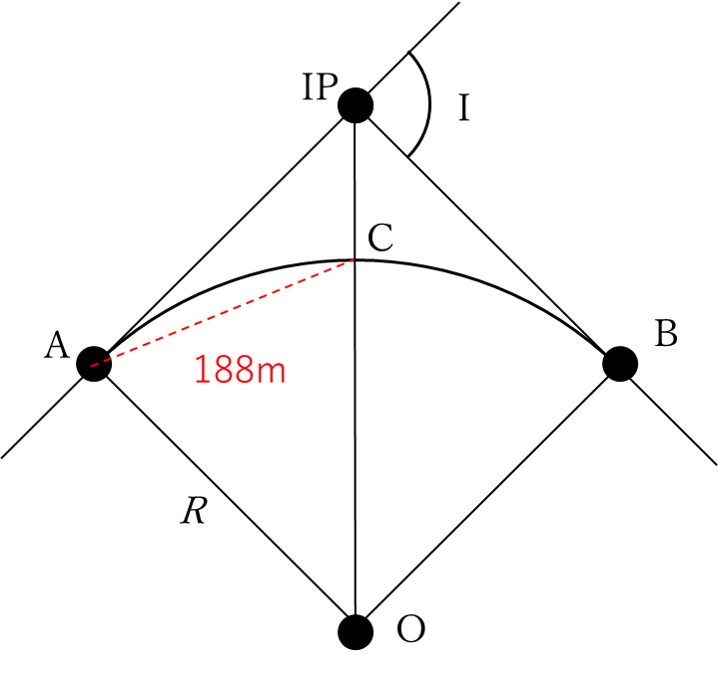
まず、今回求めたい「点Aから円曲線の中点Cまでの弦長」はコチラのことです。
この弦長を導くためには、
- 問題文からわかる数値を図に書き込む
- ∠AOCを求める
- ∠CAOもしくは∠ACOを求める
- 正弦定理を利用して弦長ACを求める
という手順が必要です。
それぞれの手順について詳しく見ていきましょう
手順1 問題文からわかる数値を図に書き込む
まずは、問題文からわかる内容を図に書き込みます。
今回の問題文からわかる内容は次の通りです。
- 曲線半径R =200 m
- 交角I =112°
また、点Aから交点IPまでの直線は円Oの接線になるので、円の接線と交差する半径の線の関係から
- ∠O-A-IP=90°(直角)
となります、
以上のことを図にまとめると次のようになります。
手順2 ∠AOCを求める
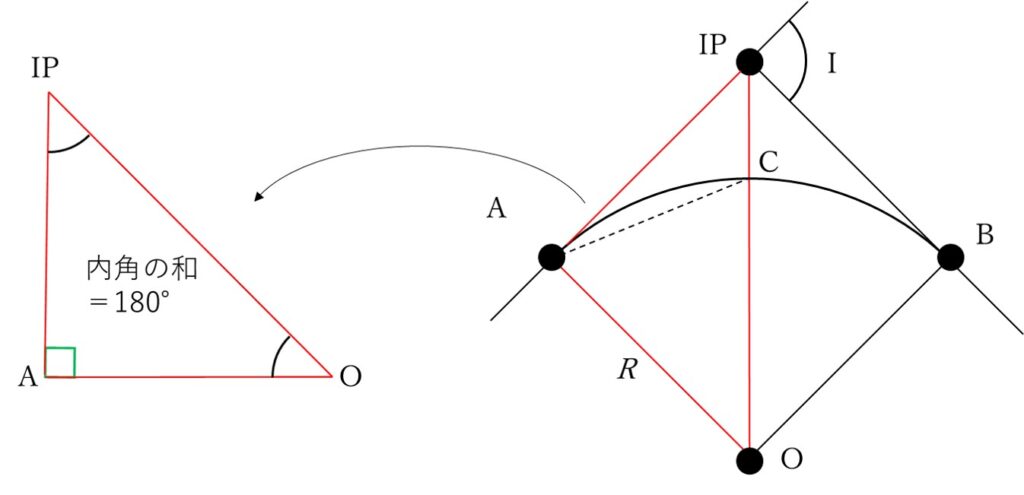
続いて、∠AOCを求めていきますが、そのために△AO-IPに注目します。
△AO-IPのうち、∠O-A-IP=90°(直角)ということがわかっていますから、残りの∠A-IP-Oがわかれば三角形の内角の和の180°を利用して∠AOCを計算できそうです。
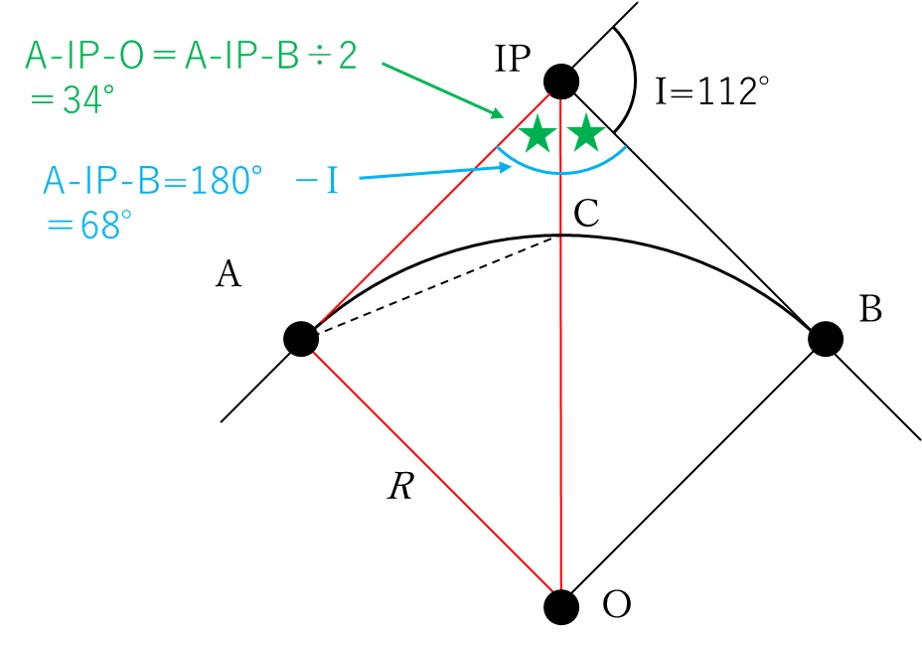
その∠A-IP-Oですが、△AO-IPと△BO-IPはIP-Oを基準に線対象なので、∠A-IP-O=∠B-IP-Oとなります。
つまり、∠A-IP-B=∠A-IP-O+∠B-IP-O=2×(∠A-IP-O)です。
∠A-IP-Bは直線の角度(180°)から交角Iを引いた値と同じなので
∠A-IP-B=180°-交角I
∠A-IP-B=2×(∠A-IP-O)、交角I=112°なので
2×(∠A-IP-O)=180°-112°
2×(∠A-IP-O)=68°
∠A-IP-O=68°÷2
∠A-IP-O=34°
と計算することができます。
続いて、∠AOCを計算するために三角形の内角の和を利用します。
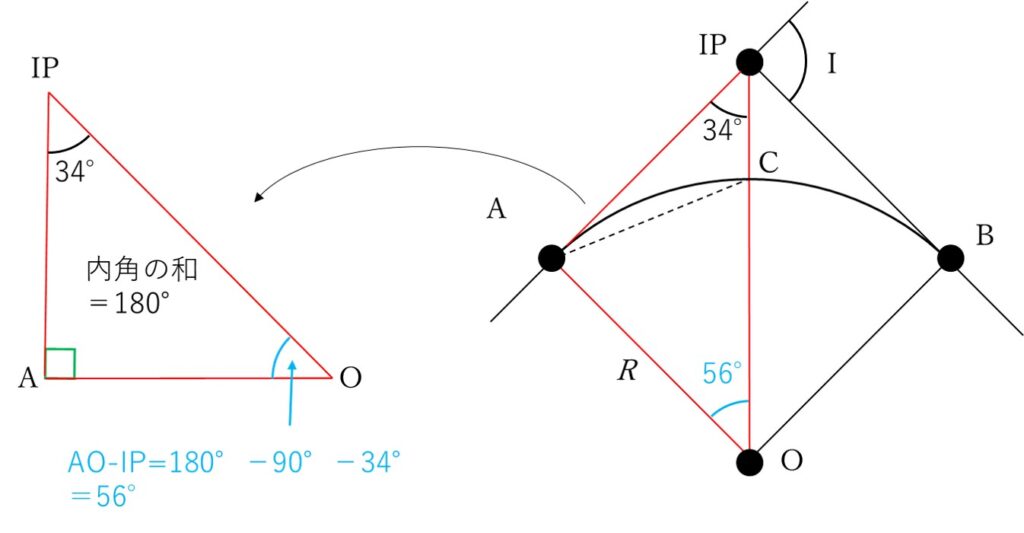
△AO-IPの角度のうち、∠O-A-IP=90°(直角)、∠A-IP-O=34°ですので
∠AO-IP+∠O-A-IP+∠A-IP-O=180°
∠AO-IP=180°-∠O-A-IP-∠A-IP-O
∠AO-IP=180°-90°-34°
∠AO-IP=56°
∠AO-IPは∠AOCと一致していますので、∠AOC=56°となります。
手順3 ∠CAOもしくは∠ACOを求める
続いて、∠CAOもしくは∠ACOのどちらかの値を求めます。
∠CAOもしくは∠ACOを求めるためには、手順2と同様に三角形の内角の和を利用します。
今回は△ACOに注目すると、AO・ACどちらも円の半径なのでAO=AC=200mとなるので二等辺三角形であることがわかります。
よって、∠CAO=∠ACOです。
あとは、△ACOの三角形の内角の和を利用するので
∠AOC+∠CAO+∠ACO=180°
∠CAO+∠ACO=180°-∠AOC
∠CAO=∠ACO、∠AOC=56°なので
2∠CAO=180°-56°
2∠CAO=124°
∠CAO=124°÷2
∠CAO=62°
よって、∠CAO=62°となります。
手順4 正弦定理を利用して弦長ACを求める
最後に、△AOCに正弦定理を用いて弦長ACを求めていきます。
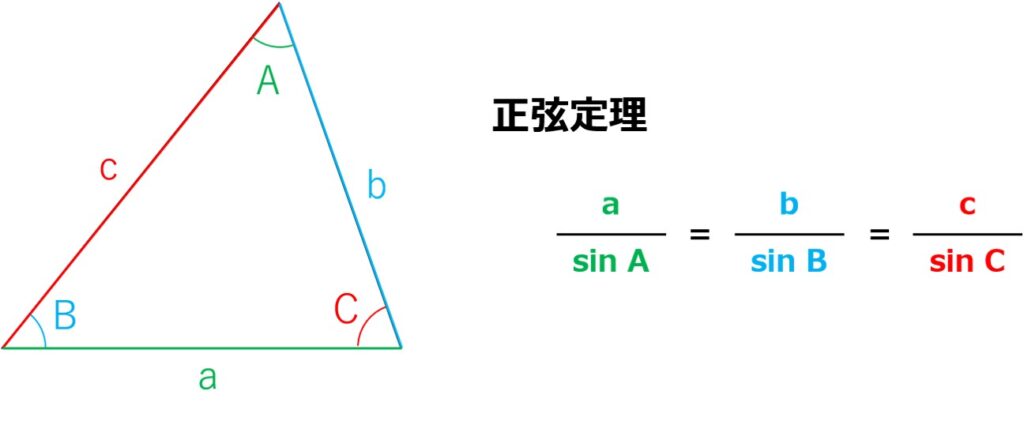
正弦定理は、下図のような関係を利用した定理のことです。
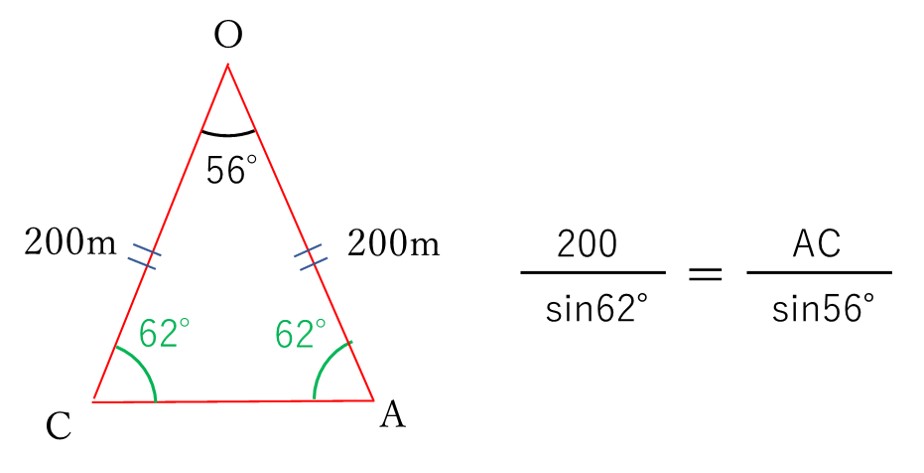
今回の問題の△AOCの場合は、下図のように当てはまります。
よって、弦長AC=Xとして正弦定理を用いると
AO/sin(∠ACO)=AC/sin(∠AOC)
200/sin(62°)=X/sin(56°)
関数表よりsin(62°)=0.8829、sin(56°)=0.8290なので
200/0.8829=X/0.8290
X=(200/0.8829)×0.8290
X=226.5262×0.8290
X=187.7902
X≒188
よって、弦長AC=188mとなります。
以上のことから正しい選択肢は「3」であるといえます。
令和2年測量士補試験No.26のまとめ
応用測量の分野からの出題でした。
曲線を含む道路の長さを求める問題は様々なパターンで出題されます。
数学の問題に近く、ときにはひらめきが必要なこともありますが、基本的には正弦定理や余弦定理を覚えておくと解ける問題が多いです。
余裕があれば様々なパターンの過去問を解き、色々な形に対応できるようにしておきましょう!
令和2年測量士補試験No.26の類題
他年度の測量士補試験に出題された本問の類題です!ぜひチャレンジしてみてください!
令和3年測量士補試験問題集NO.26→問題文及び解説記事はコチラ
令和4年測量士補試験問題集NO.25→問題文及び解説記事はコチラ
その他の測量士補試験の問題に挑戦!
令和2年のNO.26の問題を確認したら、その他の問題にも挑戦していきましょう!
本ブログでは各問題の解説を年度ごとに一覧にまとめたページがありますので、ぜひその記事からその他の問題に挑戦してみてください!
問題解説のまとめ記事はコチラからどうぞ!→【令和5年】問題解説リンク集から現役測量士の解説を読んで測量士補試験の過去問を攻略しよう!!
さいごに
本ブログを参考にしていただきありがとうございます。
内容に関して不明な点、ご質問、指摘事項、感想などございましたら、コメントやメールにてご連絡ください。
励みになるとともに、本ブログをよりたくさんの皆様に有益なものにできると考えています。
ぜひお待ちしております。
お問い合わせ先:surveyor_kenzo☆aol.com
※ご連絡の際は☆を@に変更してください。

 図25
図25