必要な用語や手法に関する解説も一緒におこなっていきますので、参考書代わりに本記事を使ってみてください。 その他の過去問の解説記事はコチラのリンクからどうぞ。
目次
令和2年測量士補試験No.25の問題文
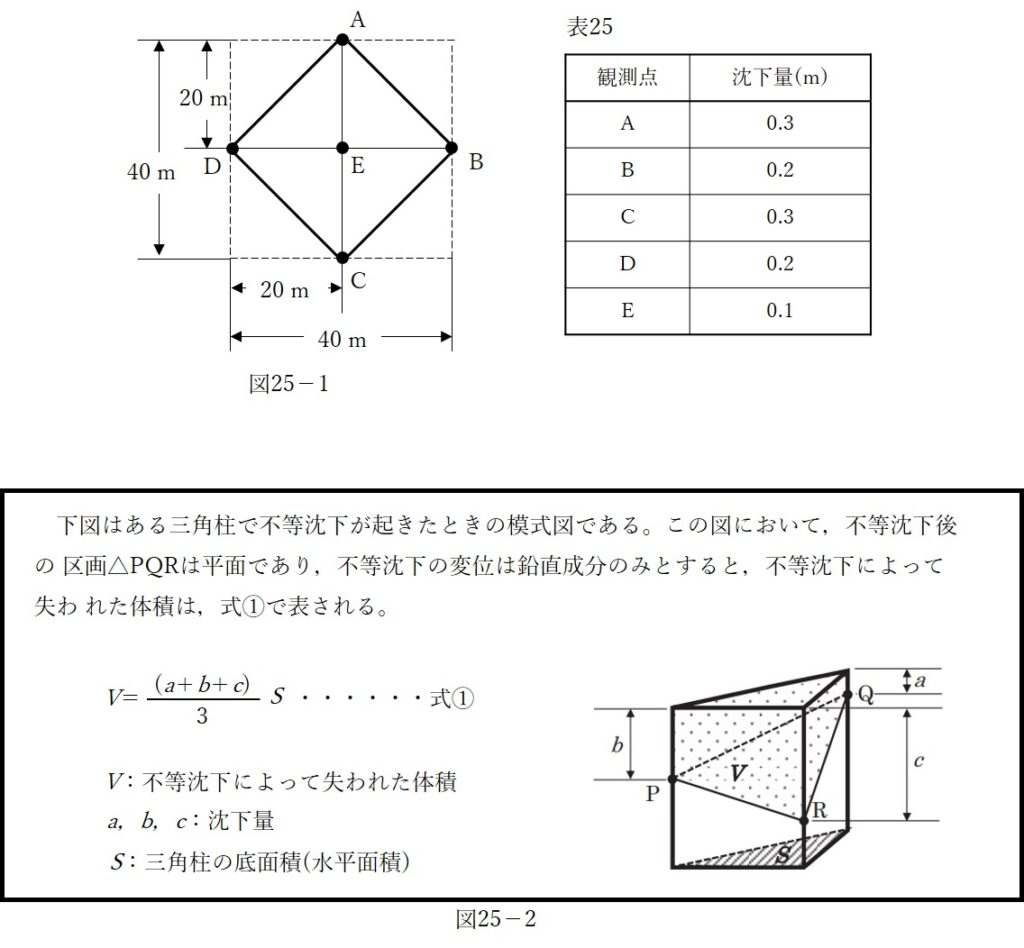
10年前に水平に整地した図25－ 1 の土地ABCDにおいて,先日,水準測量を行ったところ，地盤が不等沈下していたことが判明した。観測点の位置関係及び沈下量は，図25－ 1 及び表25に示すとおりである。盛土により，整地された元の地盤高に戻すには，どれだけの土量が必要か。図25－ 2 の式①を用いて算出し，最も近いものを次のページの中から選べ。
ただし，盛土による新たな沈下の発生は考えないものとする。
なお，関数の値が必要な場合は，巻末の関数表を使用すること。
- 140 ㎥(立方メートル)
- 160 ㎥(立方メートル)
- 180 ㎥(立方メートル)
- 200 ㎥(立方メートル)
- 400 ㎥(立方メートル)
（令和2年測量士補試験問題集 No.25）
令和2年測量士補試験No.25の解答・解説
「応用測量」の分野からの出題です。
正解は「2」となります。
以下、解答を導くまでの詳しい計算の解説です。
元の地盤に戻す土量を求めるまでの手順
本問は、沈下してしまった地盤を元に戻すための土量を求めるものです。
沈下とは、時間が経過することで地盤が段々と沈んでしまい、周囲と比べて相対的に地盤の高さが低くなってしまう現象のことです。
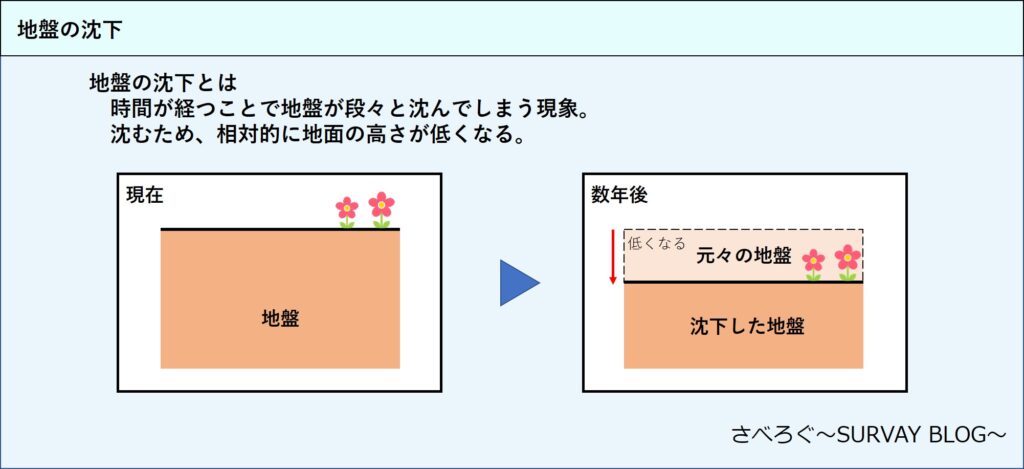地盤の高さを元に戻すためには、低くなってしまった地盤の体積分、埋める必要があります。つまり今回の問題では、地盤の沈下量を求めることができればそれが答えになるということです。
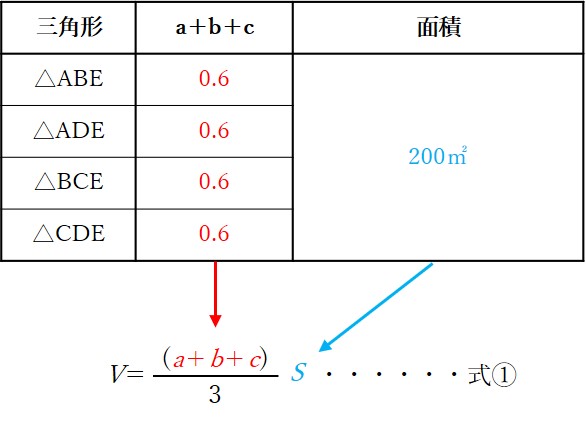
図25-2でその体積を求める式①が提示されていますので、それに合うように問題文にある数値を当てはめれば計算できます。
ただしこの式は三角柱に対する式なので、図25-1にある各三角の体積を求める必要があります。
また、式①では「三角柱の底面積S」が必要となっていますので、まずは図25-1にある各三角形の面積を求めていく必要がありそうです。
続いて、それぞれの三角形の頂点の沈下量の合計を求めれば、最終的な回答である各三角形の体積を計算できます。
よって、本問を解くための手順は
- 各三角形の面積Sを求める
- 各三角形の頂点の沈下量の合計をまとめる
- 式①に手順1,2の結果を入力して体積を計算する
となります。それぞれの手順は次に詳しく解説していきます。
手順１ 各三角形の面積Sを求める
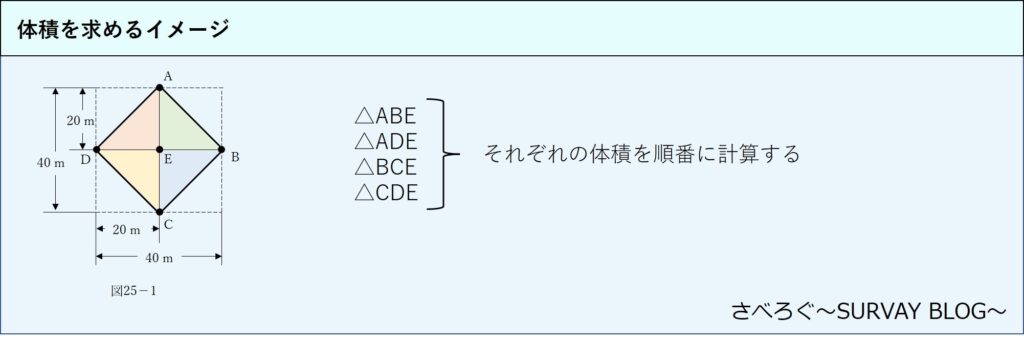
まずは、図25-1にある各三角形の面積を求めていきます。
図25-1にある三角形は以下の4つです。
- △ABE
- △ADE
- △BCE
- △CDE
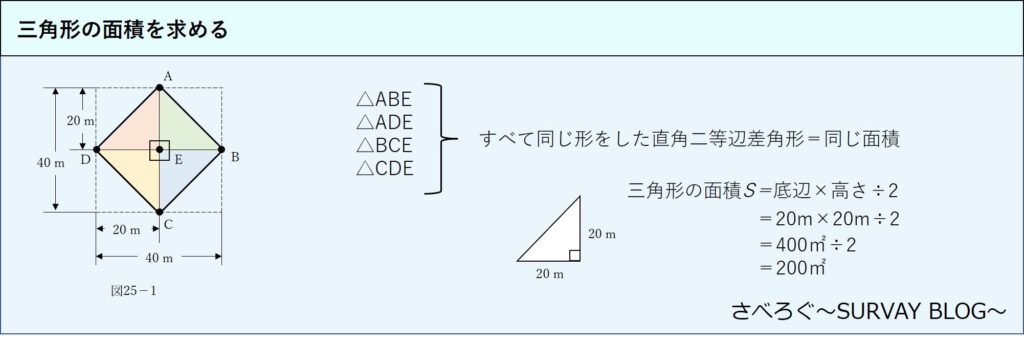
図を確認すると各三角形はすべて同じ形の直角二等辺三角形であり、等しい辺の長さは20mであることがわかります。つまり、各三角形の面積も同じです。
よって、1つの三角形の面積を計算すれば大丈夫です。計算すると次のようになります。
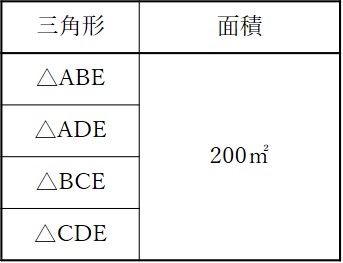
これで、各三角形の面積はすべて200㎡であることがわかりました。最後に、表にまとめておきましょう。
手順２ 各三角形の頂点の沈下量の合計をまとめる
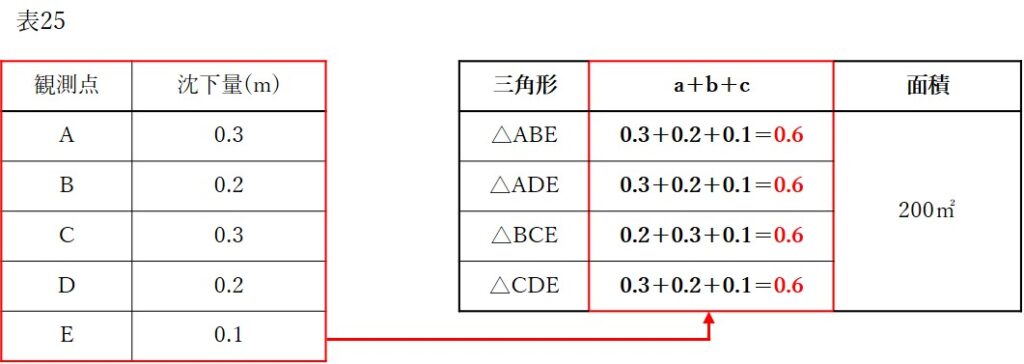
図25-2の式①にあるa，b，cはそれぞれ各三角形の頂点の場所をあらわしていて、各三角形の頂点の場所の沈下量は表25にまとめられています。
表25の数値を各三角形の頂点に当てはめて合計し、手順1で作った表の横にくっつけると、次のようにまとめることができます。
この作業は数値を選ぶミスをしやすいので、必ずまとめたあとに再度確認しましょう。
表のようにまとめると、各三角形の頂点の沈下量の合計は
- △ABEの頂点の合計沈下量＝0.3＋0.2＋0.1＝0.6
- △ADEの頂点の合計沈下量＝0.3＋0.2＋0.1＝0.6
- △BCEの頂点の合計沈下量＝0.2＋0.3＋0.1＝0.6
- △CDEの頂点の合計沈下量＝0.3＋0.2＋0.1＝0.6
とそれぞれ求めることが可能です。よって、各三角形の頂点の合計沈下量はそれぞれすべて0.6mであることがわかりました。
手順３ 式①に手順1,2の結果を入力して体積を計算する
最後に、手順１，２で計算した結果を式①に代入して、それぞれの三角形の体積を計算していきます。
例えば、△ABEを底面に持つ三角柱の体積を計算する場合は
式①はV＝{(a＋b＋c)/3}×S
a＋b＋c＝0.6m、S=200㎡なので
V=(0.6m/3)×200㎡
＝0.2m×200㎡
＝40㎥
と計算できますので、△ABEを底面に持つ三角柱の体積V=40㎥となります。
同様に△ADE、△BCE、△CDEを計算すると
△ADE、△BCE、△CDEのいずれも(a＋b＋c)＝0.6m、S＝200㎡
つまり、△ADE、△BCE、△CDEを底面に持つどの三角柱の体積も、△ABEを底面に持つ三角柱の体積と同じ値になる。
よって、
△ADEを底面に持つ三角柱の体積V=40㎥
△BCEを底面に持つ三角柱の体積V=40㎥
△CDEを底面に持つ三角柱の体積V=40㎥
となります。
あとはそれぞれの体積を足せば全体で沈下した量になるので、
全体の沈下量＝各三角中の体積の合計
＝40㎥＋40㎥＋40㎥＋40㎥
＝160㎥
となり、全体の沈下量は160㎥となります。よって、沈下した分を補い元の高さに戻すためには、160㎥の土量が必要になるので、正しい選択肢は「2」といえます。
令和2年測量士補試験No.25のまとめ
応用測量の分野からの出題でした。
土量の計算は数年に一度出るぐらいの頻度で、そこまで頻出ではありません。また、大体の問題では計算するための式がのっています。
そのため、落ち着いて順序だてて問題を解いていけば確実に得点できるものが多いです。
落とさないように、気を付けて問題を解いていきましょう！
その他の測量士補試験の問題に挑戦！
令和2年のNO.25の問題を確認したら、その他の問題にも挑戦していきましょう！
本ブログでは各問題の解説を年度ごとに一覧にまとめたページがありますので、ぜひその記事からその他の問題に挑戦してみてください！
問題解説のまとめ記事はコチラからどうぞ！→【令和5年】問題解説リンク集から現役測量士の解説を読んで測量士補試験の過去問を攻略しよう！！
さいごに
本ブログを参考にしていただきありがとうございます。
内容に関して不明な点、ご質問、指摘事項、感想などございましたら、コメントやメールにてご連絡ください。
励みになるとともに、本ブログをよりたくさんの皆様に有益なものにできると考えています。
ぜひお待ちしております。
お問い合わせ先：surveyor_kenzo☆aol.com
※ご連絡の際は☆を@に変更してください。