必要な用語や手法に関する解説も一緒におこなっていきますので、参考書代わりに本記事を使ってみてください。
目次
令和3年測量士補試験No.8の問題文
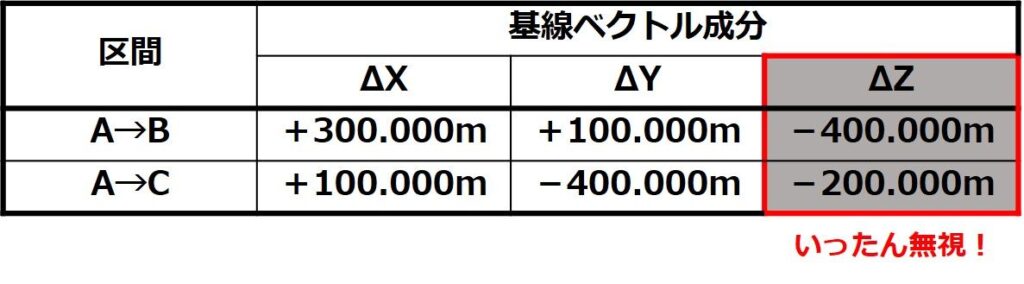
GNSS 測量機を用いた基準点測量を行い,基線解析により基準点 A から基準点 B,基準点 Aから基準点 C までの基線ベクトルを得た。表8は,地心直交座標系(平成 14 年国土交通省告示第 185 号)における X 軸,Y 軸,Z 軸方向について,それぞれの基線ベクトル成分(ΔX,ΔY,ΔZ)を示したものである。基準点 C から基準点 B までの斜距離は幾らか。最も近いものを次の中から選べ。
なお,関数の値が必要な場合は,巻末の関数表を使用すること。(表8)
(回答群)
1.538.516 m
2.574.456 m
3.781.025 m
4.806.226 m
5.877.496 m(令和3年測量士補試験問題集 No8より)
令和3年測量士補試験No.8の解答・解説
「汎地球測位システム測量」の分野からの出題です。
解答は「2」となります。以下、詳しい手順の解説です。
解答を得るまでの計算手順
基準点 C から基準点 B までの斜距離を出すには、以下の手順を踏む必要があります。
- XY平面上に基準点A、B、Cを配置する
- XY平面上のBC間の距離を出す
- 基準点B、Cの高さを考える
- 三平方の定理でBCの斜距離を出す
X、Y、Zの軸があるので三次元の斜距離の計算となるので少し計算しづらそうに感じます。
しかしながら、落ち着いて二次元に分解して計算すれば大丈夫です!
それぞれの詳しい手順の解説を見てみましょう!
1.XY平面上に基準点A、B、Cを配置する
三次元の斜距離の計算はそのままでは計算しづらいので、まずは二次元に落とし込んで考えてみます。
表では「区間A→B」と「区間A→C」の基線ベクトル成分が書いてあります。
基線ベクトル成分という難しい言葉で書いてありますが要は「自分がいる位置からそれぞれの方向にどのくらい離れているか」を表しています。
例えば「区間A→CのΔX=+300.000m、ΔY=+100.000m」の場合は「基準点Aに立ったときにX方向に+300.000m、Y方向に+100.000m進んだところに地点Cがある」ということになります。
言い換えれば、A=(0,0)、C=(+300.000,+100.000)の座標としても考えることができるということです。
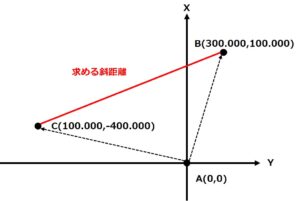
今回の問題では「区間A→B」と「区間A→C」の基線ベクトル成分が書いてあるので、A=(0,0)の原点としてB=(+300.000,+100.000)、C=(+100.000,-400.000)の座標として考えましょう。
2.XY平面上のBC間の距離を出す
前回の手順で基準点A、B、Cの位置をXY平面上に配置したので、今度はそのXY平面上での基準点BとCの間の距離(斜距離d1とします)を求めてみます。
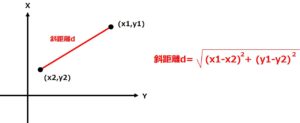
斜距離を求める式は以下の図の通りです。
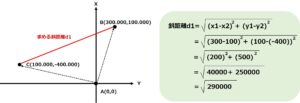
この式に今回の座標を当てはめると次のように求められます。
よって、d1=√290000となります。
3.基準点B、Cの高さを考える
手順1,2ではXY平面上について考えました。
この手順では基準点Bと基準点CのZ方向(高さ)の差について考えてみます。
高さの差について考えるだけなので、XとYの座標は関係ありません。
素直に基準点Bと基準点CのZ座標の差(Z1とします)を出してあげるだけで大丈夫です。
よってこれを計算すると
Z1=(基準点BのZ座標)-(基準点CのZ座標)
=-400-(-200)
=-400+200
=-200
高さの差が分かれば良いので-200から-の符号を取っちゃいます。
よってZ1=200となります。
4.三平方の定理でBCの斜距離を出す
これまでの手順によって
- 手順2でXY平面上のBC間の距離
- 手順3で基準点BとCの高さの差
をそれぞれ求めました。
これによって、BC間の斜距離(d2とします)を求めることができます。
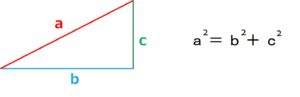
BC間の斜距離(d2)は三平方の定理を利用することで求めることが可能です。
三平方の定理とはこんなやつですね。
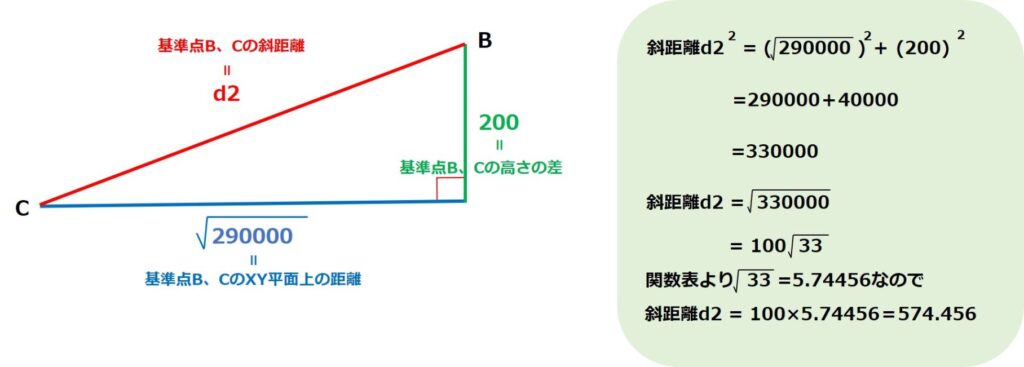
これを今回の問題に当てはめると、
となります。
よってBC=574.456mです。
令和3年測量士補試験No.8のまとめ
「汎地球測位システム測量」からの出題でした。
本問題は三次元の位置関係をイメージする必要があるので、少しとっかかりにくかった方もいるかもしれません。
しかしながら、落ち着いてそれぞれの水平距離や高さを2次元で考えることができれば問題ありませんよ!
何度か類似の問題を解くことで、イメージ力の向上にもつながります。
こういった問題は出題頻度が高いので、ぜひ貴重な得点源にしてください!
その他の測量士補試験の問題に挑戦!
令和3年のNO.8の問題を確認したら、その他の問題にも挑戦していきましょう!
本ブログでは各問題の解説を年度ごとに一覧にまとめたページがありますので、ぜひその記事からその他の問題に挑戦してみてください!
問題解説のまとめ記事はコチラからどうぞ!→過去問に挑戦!現役測量士の解説を読んで測量士補試験を攻略しよう!
さいごに
本ブログを参考にしていただきありがとうございます。
内容に関して不明な点、ご質問、指摘事項、感想などございましたら、コメントやメールにてご連絡ください。
励みになるとともに、本ブログをよりたくさんの皆様に有益なものにできると考えています。
ぜひお待ちしております。
お問い合わせ先:surveyor_kenzo☆aol.com
※ご連絡の際は☆を@に変更してください。