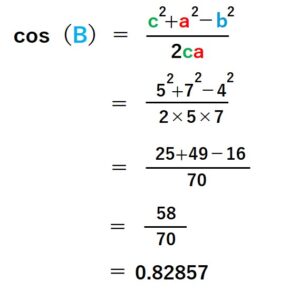必要な用語や手法に関する解説も一緒におこなっていきますので、参考書代わりに本記事を使ってみてください。
目次
令和2年測量士補試験No.3の問題文
次の a ~ c の各問の答えとして最も近いものの組合せはどれか。次の中から選べ。
ただし,円周率π=3.14とする。
なお,関数の値が必要な場合は,巻末の関数表を使用すること。
- 30°11′26″を10進法に換算すると幾らか。
- 120°をラジアンに換算すると幾らか。
- 三角形ABCで辺AB=5.0 m,辺BC=7.0 m,辺AC=4.0 mとしたとき,∠ABCの角度は幾らか。
- (a)30.19055°(b)1.05ラジアン(c)44°
- (a)30.19055°(b)2.09ラジアン(c)34°
- (a)30.19055°(b)2.09ラジアン(c)44°
- (a)30.61666°(b)1.05ラジアン(c)34°
- (a)30.61666°(b)2.09ラジアン(c)44°
(令和2年測量士補試験問題集 No.3)
令和2年測量士補試験No.3の解答・解説
「測量に関する法規」の分野からの出題です。
解答は「2」となります。以下、(a)~(c)の各計算の詳しい解説です。
計算に使用する関数表はコチラを参考にしてください。→関数表
(a)60進法→10進法への換算の計算
(a)は「30°11′26″を10進法に換算すると幾らか。」という問題です。
10進法と60進法
まず、10進法とは0から順番に数えていき、10を区切りに位(くらい)を上げる数字の表現方法です。
普段ぼくやあなたが使用している数字のほとんどは10進法ですね。逆に10進法じゃないのものでイメージしやすいのは時計です。
時計の場合は、60秒=1分、60分=1時間と0から数え始めて60までいくごとに位(くらい)が1つ上がっています。
この時計のように60ごとに位が上がる表現方法は60進法と呼ばれます。
今回の問題で出てくる「30°11′26″」も60ごとに位(くらい)が変わるので60進法です。
60進法から10進法へ変換する方法
今回の問題は「60進法から10進法に変換すること」を求められています。
「60進法から10進法に変換する」ということは「30°11′26″」を「30.○○○°」と°(度)′(分)″(秒)を使用せずに小数点を使用して表現するということです。
それでは、60進法から10進法へはどのように変換すればよいのでしょうか?手順は次の通りです。
- °(度)′(分)″(秒)のうち、′(分)″(秒)を°(度)へ変換する。
- ′(分)″(秒)から変換した°(度)の値を、最初からある°(度)へ足す
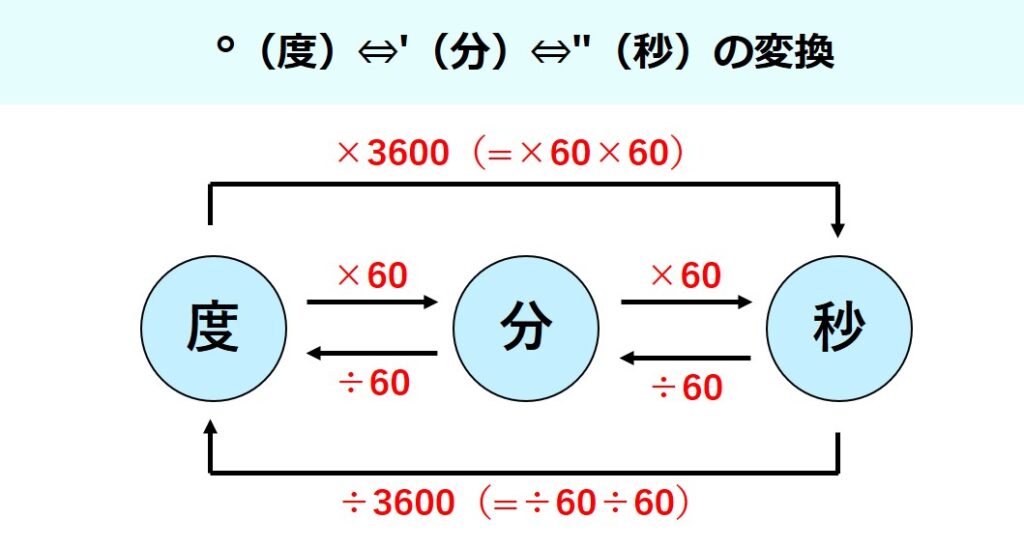
また、°(度)′(分)″(秒)のそれぞれの変換の関係性は次の通りです。60進法なので「60」という数字を利用して変換していきます。
変換の関係性を図で表すと以下のようになります。
それでは、実際に手順をあてはめて、問題を解いてみましょう!
30°11′26″を10進法の表現に変換する
まずは、30°11′26″のうち、11′26″の部分を°(度)へ変換します。
″(秒)→°(度)、′(分)→°(度)の関係はそれぞれ次の通りです。
- ″(秒)→°(度):″(秒)の値を3600でわる
- ′(分)→°(度):′(分)の値を60でわる
よって、11′26″を度に変換すると
11′→(11/60)°≒0.18333
26″→(26/3600)°≒0.00722
となります。
あとはそれぞれ変換して導き出した°(度)の数値と元からある°(度)の数値をたすだけです。よって
30°+0.18333°+0.00722°
=30.19
となりますので、30°11′26″を10進法で表した値は30.19055°となります。
(b)度(度数法)→ラジアン(弧度法)への変換の計算
(b)は「120°をラジアンに換算すると幾らか。」という問題です。
度数法と弧度法
測量士補試験では、角度を表す方法に「度数法」と「弧度法」の2つが出てきます。
度数法は一般の人が最もなじみ深い0~360の間の数字で「〇°」と表すものです。
一方で弧度法は0~2πの間で「〇rad(ラジアン)」と表すものです。
また、度数法でいう180°は弧度法でいうπとなります。つまり「180°=π rad」です。
度数法→弧度法への変換
今回の問題は「度数法から弧度法に変換すること」を求められています。
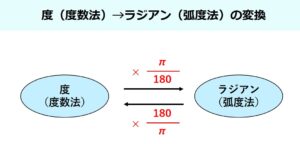
前述したとおり「180°=π rad」ですので、度数法と弧度法の変換の関係性は次のようになります。
つまり、度数法(〇°)→弧度法(〇rad)に変換するためには〇°に「π/180」をかければ良いということになります。
120°を弧度法の表現に変換する
前述したとおり度数法(〇°)に「π/180」をかければ弧度法の表現に変換することができます。
今回は120°を弧度法で表せばよいので、
120°×(π/180)
を計算すれば大丈夫です。
問題文から「π=3.14」とわかりますので
120°×(π/180)
=120°×(3.14/180)
≒120°×0.017444
≒2.09
と計算できます。
よって120°を弧度法で表すと2.09となります。
(c)3つの辺の値がわかる三角形の角度計算
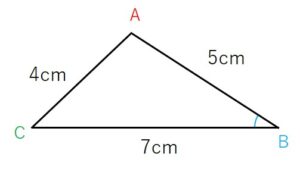
(c)は「三角形ABCで辺AB=5.0 m,辺BC=7.0 m,辺AC=4.0 mとしたとき,∠ABCの角度は幾らか。」という問題です。
3つの辺の値がわかる三角形の角度計算の方法
3つの辺の値がわかっている三角形の場合は「余弦定理」を利用すれば各角度を求めることが可能です。
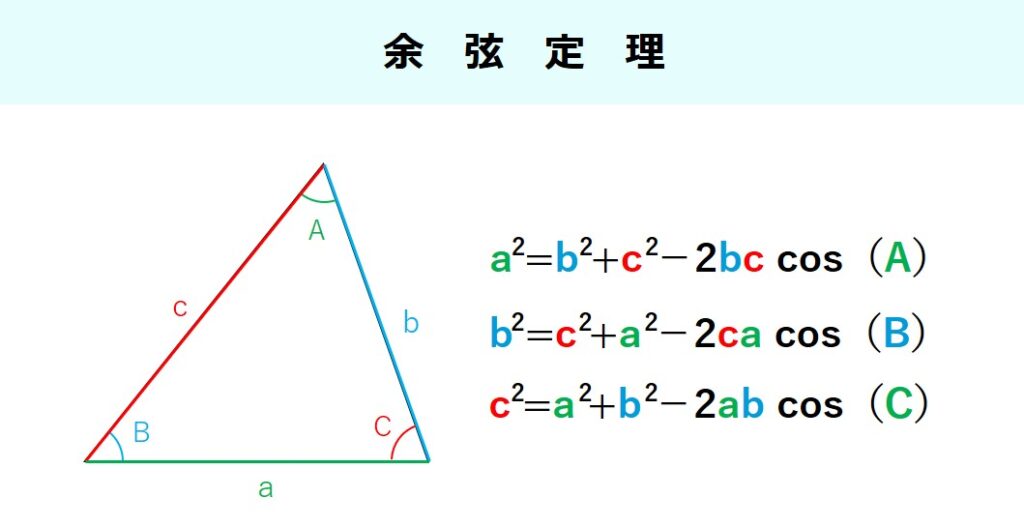
余弦定理とは「三角形の2つの辺とその間の角度が分かっていればもう1つの辺を求めることができる定理」のことです。
言い換えれば「三角形の3つの辺がわかっていれば任意の角度を求めることができる」とも言えます。
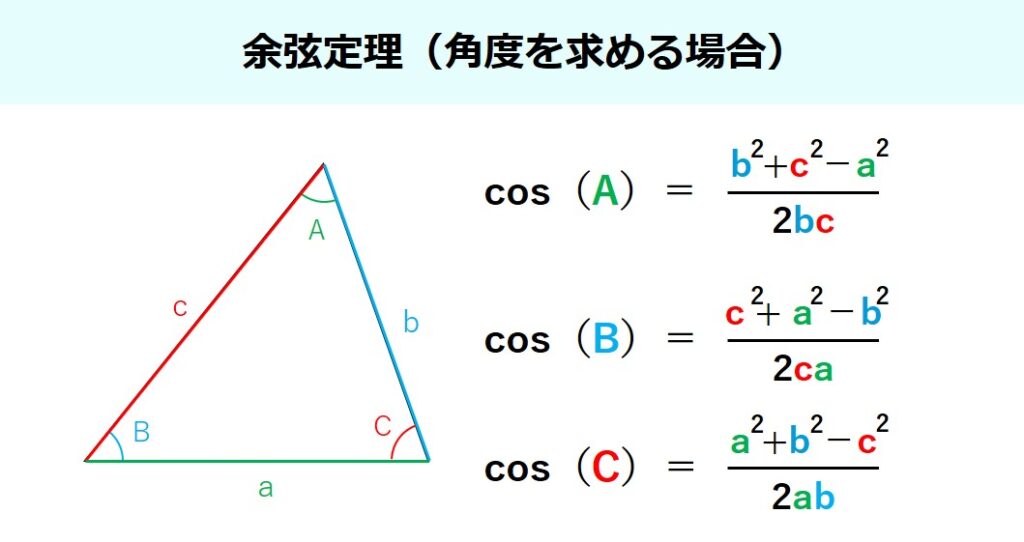
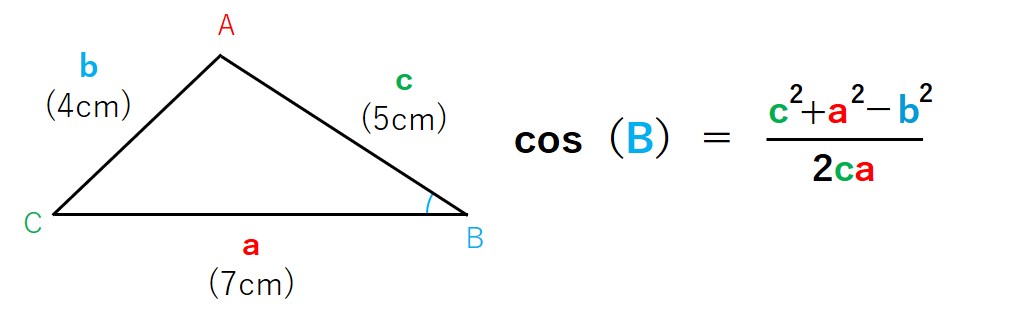
実際に角度を求めるための式に変換すると下図のような感じですね。
この余弦定理を利用して、実際に問題を解いてみましょう!
問題文の図形をイメージする
∠ABCの角度を計算する前に、まずは問題文の図形をイメージして図で表します。
どう計算すればよいかわかりやすくなりますし、計算間違いがあったときに原因を見つけやすいですからね。
問題文から
- 辺AB=5.0 m
- 辺BC=7.0 m
- 辺AC=4.0 m
- ∠ABCを求める
とわかっていますから、それらを図にすると次のようになります。
あとは、この図をもとに余弦定理をあてはめて解いていくだけです!
∠ABCを計算する
三角形ABCの∠ABCを求めたいので、前述した余弦定理(角度を求める場合)を利用して計算していきます。∠ABC=Bとすると下図のようになります。
計算結果は以下の通りです。
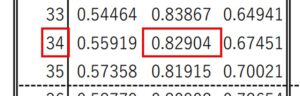
よって、COS(B)=0.82857となることがわかったので、あとは関数表から0.082857の値に近いCOS(B)を探し当てます。
関数表を参考にしていくとCOS(34°)が当てはまりそうです。
よって∠ABC=34°となります。
(a)~(c)解答のまとめ
(a)~(c)までの問題を解いていき、それぞれの解答が以下のようになりました。
- 30°11′26″を10進法で表した値は「30.19055°」
- 120°を弧度法で表すと「2.09」
- ∠ABCの角度は「34°」
上記すべての条件を満たす選択肢は「2」となりますので、正しい回答は「2」であると考えられます。
令和2年測量士補試験No.3のまとめ
「測量に関する法規」からの出題でした。
本問題では測量士補試験で基礎的な計算の要素である
- 60進法→10進法の換算
- 度進法→弧度法の換算
- 角度の計算
が出題されていました。
この問題をマスターすることはそのまま他の問題への応用が利くことになりますので、必ず押さえておきましょう!
さいごに
さべろぐでは、測量士補試験合格を目指す人を応援しています!
受験に関する相談事や、内容に関して不明な点、ご質問、指摘事項、感想などございましたら、コメントやメールにてご連絡ください。
励みになるとともに、本ブログをよりたくさんの皆様に有益なものにできると考えています。
ぜひお待ちしております。
お問い合わせ先:surveyor_kenzo☆aol.com
※ご連絡の際は☆を@に変更してください。