必要な用語や手法に関する解説も一緒におこなっていきますので、参考書代わりに本記事を使ってみてください。
目次
令和3年測量士補試験No.9の問題文
公共測量の2級基準点測量において,電子基準点 A,B を既知点とし,新点 C に GNSS 測量機を設置して観測を行った後,セミ・ダイナミック補正を適用して元期における新点 C の Y 座標値を求めたい。基線解析で得た基線ベクトルに測定誤差は含まれないものとし,基線 AC から
点 C の Y 座標値を求めることとする。
元期における電子基準点 A の Y 座標値,観測された電子基準点 A から新点 C までの基線ベクトルの Y 成分,観測時点で使用するべき地殻変動補正パラメータから求めた各点の補正量がそれぞれ表9−1,9−2,9−3のとおり与えられるとき,元期における新点 C の Y 座標値は幾らか。最も近いものを次の中から選べ。
ただし,座標値は平面直角座標系(平成 14 年国土交通省告示第9号)における値で,点 A,C の X 座標値及び楕円体高は同一とする。
また,地殻変動補正パラメータから求めた X 方向および楕円体高の補正量は考慮しないものとする。
なお,関数の値が必要な場合は,巻末の関数表を使用すること。
(回答群)
1.14,999.980 m
2.15,000.010 m
3.15,000.040 m
4.15,000.070 m
5.15,000.100 m(令和3年測量士補試験問題集 No9より)
令和3年測量士補試験No.9の解答・解説
「汎地球測位システム測量」の分野からの出題です。
解答は「1」となります。以下、詳しい手順の解説です。
関数表についてはコチラを参考にしてください。→関数表
0.まずはセミ・ダイナミック補正について理解する
セミ・ダイナミック補正については問題ありません!という方はこの章を飛ばしていただいて大丈夫です。
この問題を解くためには、まずはセミ・ダイナミック補正について理解することが大切です。
詳しい内容はまた別の記事でまとめていきますので、本章では簡単に解説します。
セミ・ダイナミック補正とは「基準日に測量した座標と、今回測量した座標で発生したズレ」を補正することです。
地殻変動の影響で、地球上の位置は少しずつ移動しています。
そのため同じ地点を違う年で測った場合に、その座標にズレが生じてしまうのです。
また、2022年3月現在の基準日は「測地成果2011」の測量成果のもので、地域によって2011年5月24日と1997年1月1日にわかれています。
この基準日の時点を元期、それ以降の測量した時点を今期と呼びます。
今期時点の測量成果にセミ・ダイナミック補正のパラメータを適用することで、元期時点の測量成果に変換することが可能です。
セミ・ダイナミック補正については国土地理院のHPでも詳しく解説されています。
少し小難しいかもしれませんが、理解していない方は一度確認してみてください。→セミ・ダイナミック補正(国土地理院)
1.元期と今期それぞれの基準点A、Cの位置関係をイメージする
今回求めたい答えは「元期における新点CのY座標値」です。
この新点CのY座標値をイメージしやすいように、元期・今期それぞれの時点での基準点A、Cの位置関係を考えてみます。
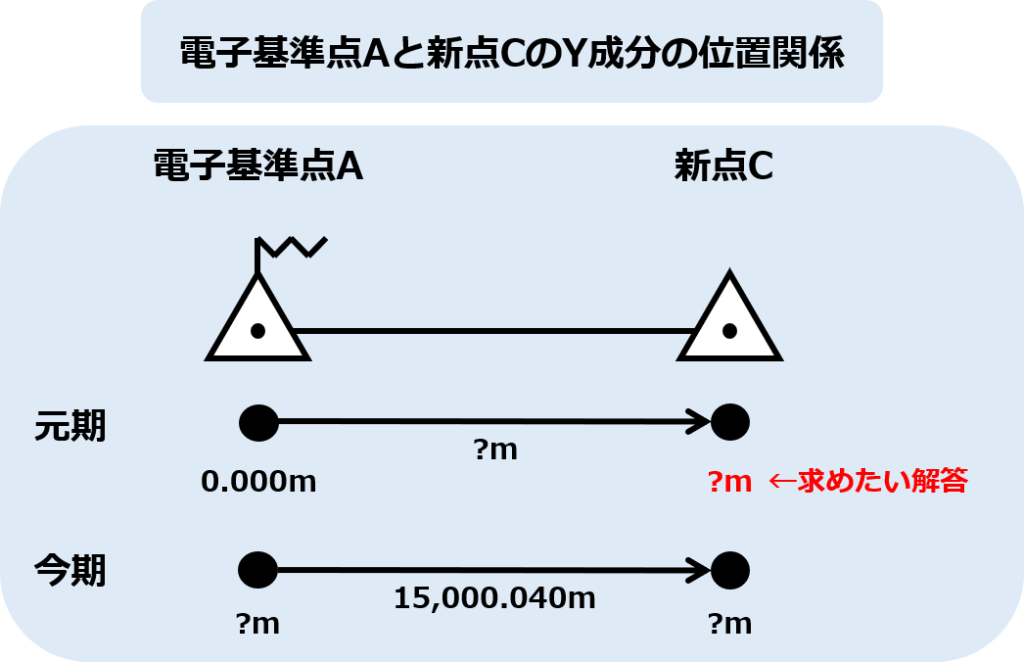
まず、表9-1と9-2から
- 電子基準点Aの元期におけるY座標値が0.000m
- 基線A→Cの基線ベクトルのY成分が15,000.040m
であることがわかっています。
また、基準点Aと新点Cは今回の観測内容なので「基線A→Cの基線ベクトルのY成分」は新点として扱います。
これらを考慮して元期・今期それぞれの位置関係をイメージするとこんな感じです。
2.今期→元期への補正量を考える
ここでさらに表9-3の内容について考えてみます。
表9-3では「元期→今期」に変換するための補正量が載っています。
- 電子基準点Aを元期→今期に変換するためには「-0.030m」の補正量
- 新点Cを元期→今期に変換するためには「0.030m」の補正量
がそれぞれ必要ということがわかりますね。
今回の問題では「元期における新点CのY座標値」の数値が欲しいので今期→元期の補正量が欲しい所です…。
表9-3から元期→今期の補正量はわかっているので、逆の数値で補正してあげれば今期→元期の補正量になりそうですね。
つまり、
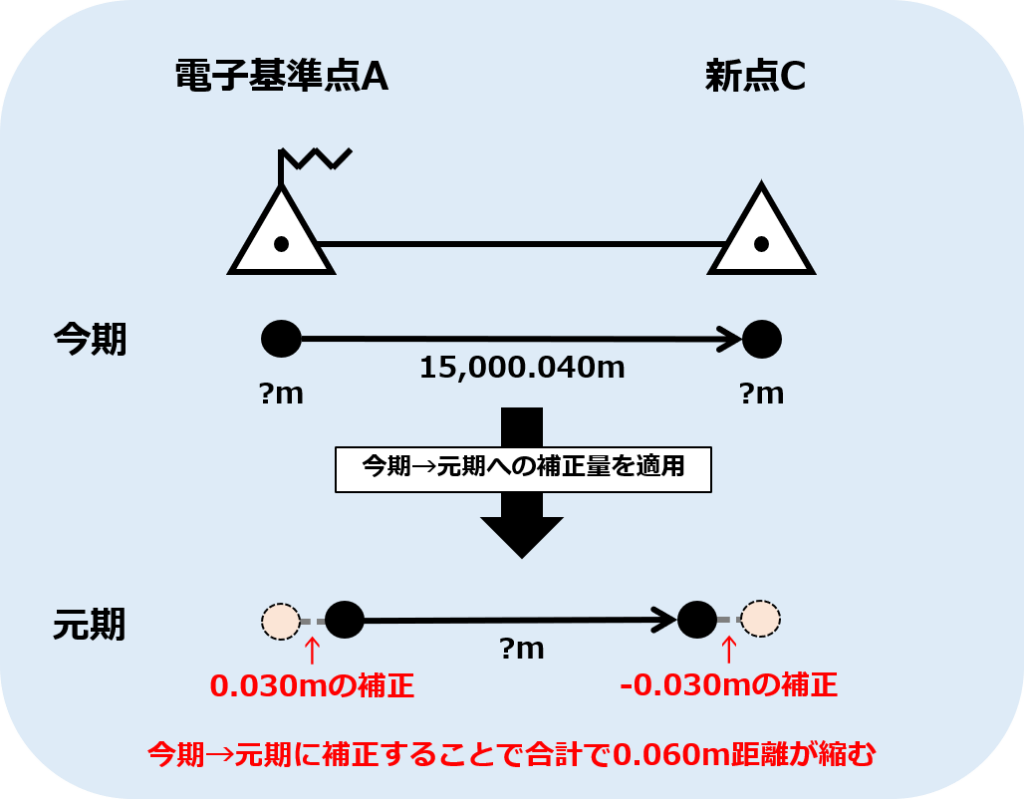
- 電子基準点Aを今期→元期に変換するためには「0.030m」
- 新点Cを今期→元期に変換するためには「-0.030m」
がそれぞれの補正量になるということです。
これを実際に表9-2の基準点Aと新点CのY成分の位置関係に当てはめてみるとこんな感じです。
3.今期におけるA→CのY成分を補正する
基準点Aと新点Cの位置をそれぞれ今期→元期で補正した結果、Y成分の距離が合計で0.060m縮むことがわかりました。
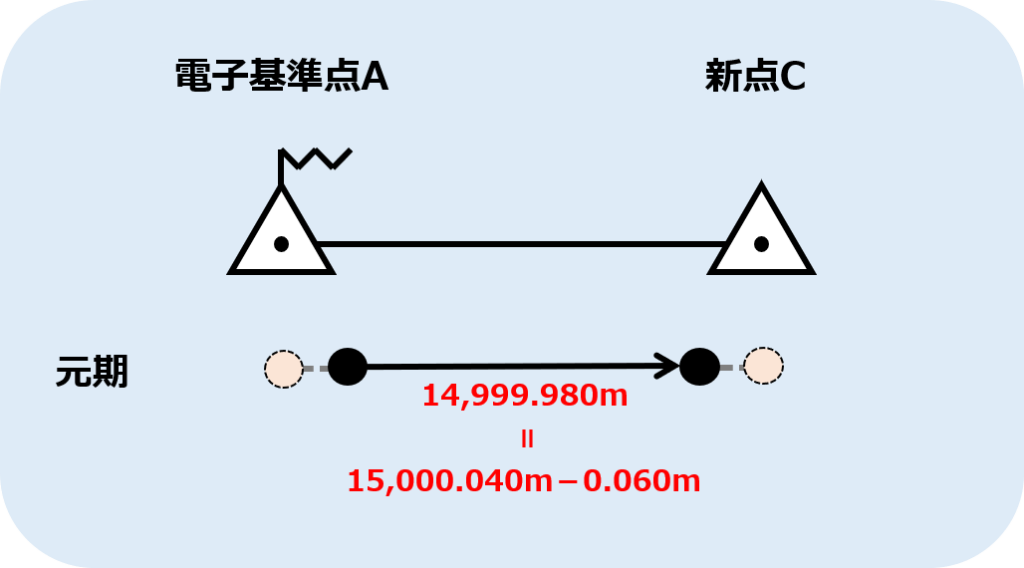
つまり、今期のA→CのY成分の15,000.040mから0.060mの長さを引くことで、元期におけるA→CのY成分が出てきます。
よって
元期におけるA→CのY成分=15,000.040m-0.060m
=14,999.980m
となります。
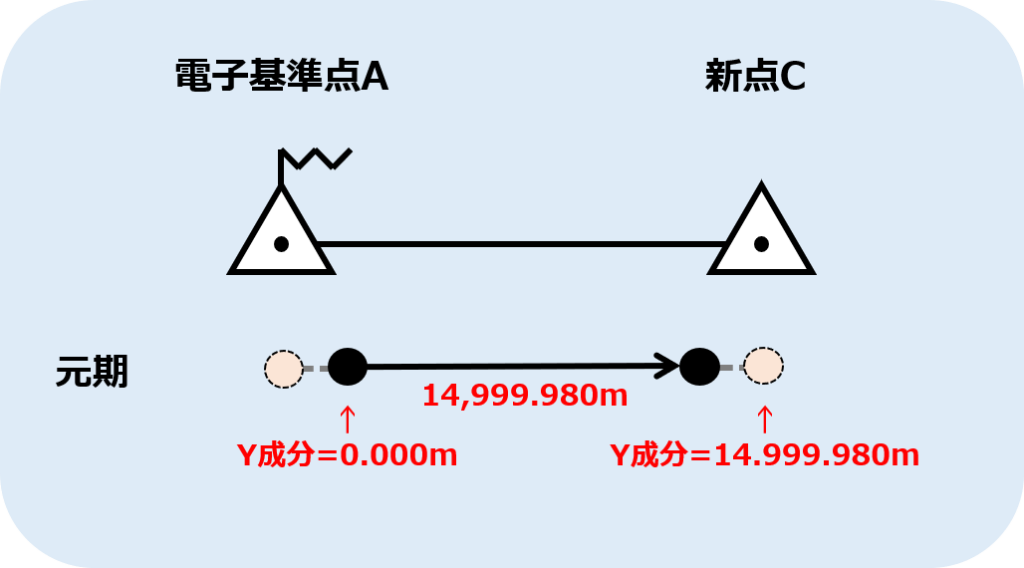
手順1で表9-1から「元期における電子基準点AのY座標値が0.000m」であることがわかっていますので、そこに元期におけるA→CのY成分=14,999.980mを当てはめると、以下の図のような感じになります。
電子基準点Aが0.000mなのでA→CのY成分の方向に14,999.980m移動すれば新点CのY成分は14,999.980mになりますね。
よって元期における新点 C の Y 座標値は「14,999.980m」であることがわかりました。
よって正しい選択肢は「1」となります。
令和3年測量士補試験No.9のまとめ
「汎地球測位システム測量」からの出題でした。
セミ・ダイナミック補正という名前に難しそうなイメージを感じた方もいらっしゃるのではないでしょうか?
しかしながら位置関係と補正の関係さえわかれば計算自体はとても単純です。
セミ・ダイナミック補正に関する内容は毎年出るものではありませんが、覚えておいて損はありません。
いざ本番で出題されたときに慌てないように、解答手順をしっかりと把握しておきましょう!
令和3年測量士補試験No.9の類題
過去に出題された本問の類題です!ぜひチャレンジしてみてください!
令和2年測量士補試験問題集NO.9→問題文及び解説記事はコチラ
その他の測量士補試験の問題に挑戦!
令和3年のNO.9の問題を確認したら、その他の問題にも挑戦していきましょう!
本ブログでは各問題の解説を年度ごとに一覧にまとめたページがありますので、ぜひその記事からその他の問題に挑戦してみてください!
問題解説のまとめ記事はコチラからどうぞ!→過去問に挑戦!現役測量士の解説を読んで測量士補試験を攻略しよう!
さいごに
本ブログを参考にしていただきありがとうございます。
内容に関して不明な点、ご質問、指摘事項、感想などございましたら、コメントやメールにてご連絡ください。
励みになるとともに、本ブログをよりたくさんの皆様に有益なものにできると考えています。
ぜひお待ちしております。
お問い合わせ先:surveyor_kenzo☆aol.com
※ご連絡の際は☆を@に変更してください。