必要な用語や手法に関する解説も一緒におこなっていきますので、参考書代わりに本記事を使ってみてください。
目次
令和2年測量士補試験No.14の問題文
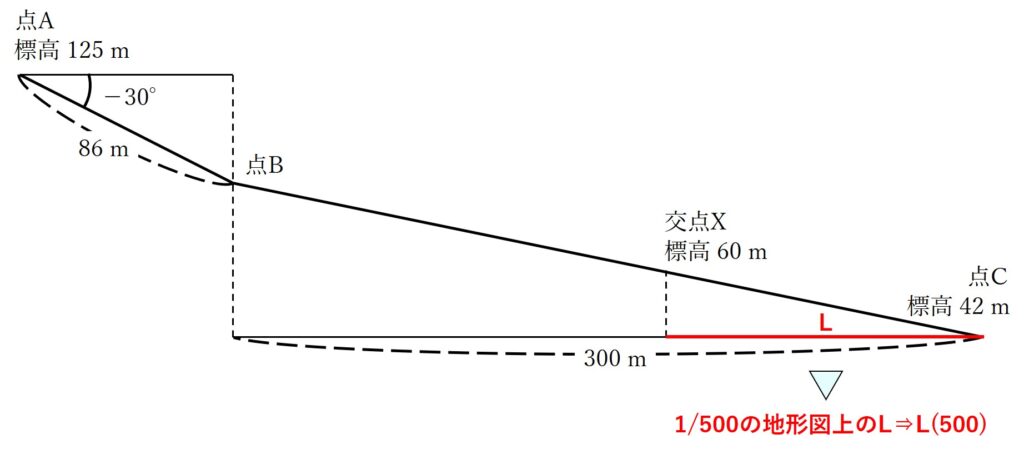
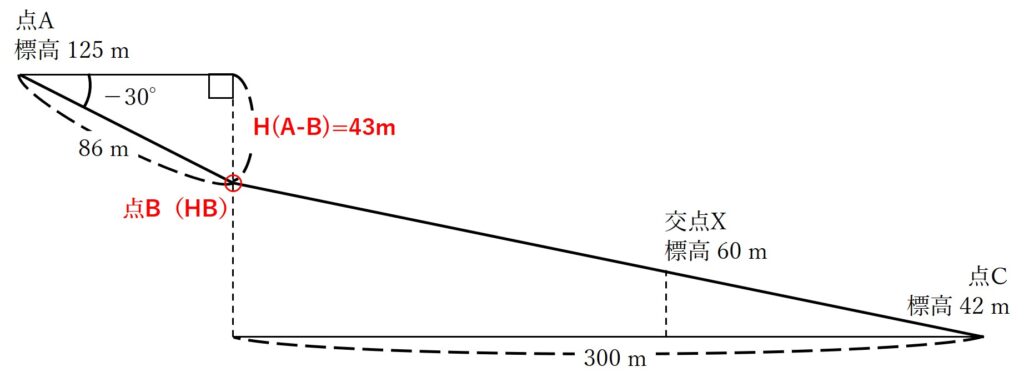
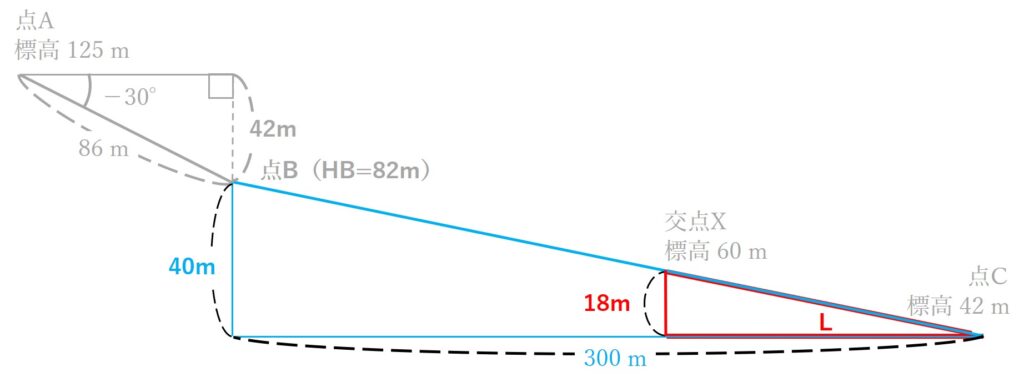
図14は,ある道路の縦断面を模式的に示したものである。この道路において,トータルステーションを用いた縮尺 1/500の地形図作成を行うため,標高125 mの点Aにトータルステーションを設置し点Bの観測を行ったところ,高低角-30°,斜距離86 mの結果を得た。また,同じ
道路上にある点Cの標高は42 mであった。点Bと点Cを結ぶ道路は,傾斜が一定でまっすぐな道路である。このとき,点B,C間の水平距離を300 mとすると,点Bと点Cを結ぶ道路とこれを横断する標高60 mの等高線との交点Xは,この地形図上で点Cから何cmの地点か。最も近いものを次の中から選べ。
なお,関数の値が必要な場合は,巻末の関数表を使用すること。
- 8.6 cm
- 13.5 cm
- 16.2 cm
- 27.0 cm
- 33.0 cm
(令和2年測量士補試験問題集 No.14)
令和2年測量士補試験No.14の解答・解説
「水準測量」の分野からの出題です。
解答は「4」となります。以下、解答を導く詳しい計算手順と考え方です。
計算に使用する関数表はコチラを参考にしてください。→関数表
1/500地形図上の点Cから交点Xまでの距離を求めるまでの計算手順
本問では、点Cから交点Xまでの距離が1/500の地形図上では何cmになるかを求めることが目的となっています。今回は求める実際の点Cと交点Xまでの距離をLとし、1/500の地形図上のLの数値をL(500)とします。
L(500)を導くまでの手順は
- 点Bの標高を求める
- 点Cと点B及び点Cと点Xの標高の差を求める
- 点Cから点Xまでの距離Lを求める
- 1/500の地形図上のL(500)を求める
となっており、それぞれの手順では三角関数や三角形の相似の計算を使用します。
数学の問題に近いので、気負いせず落ち着いて解いていきましょう。
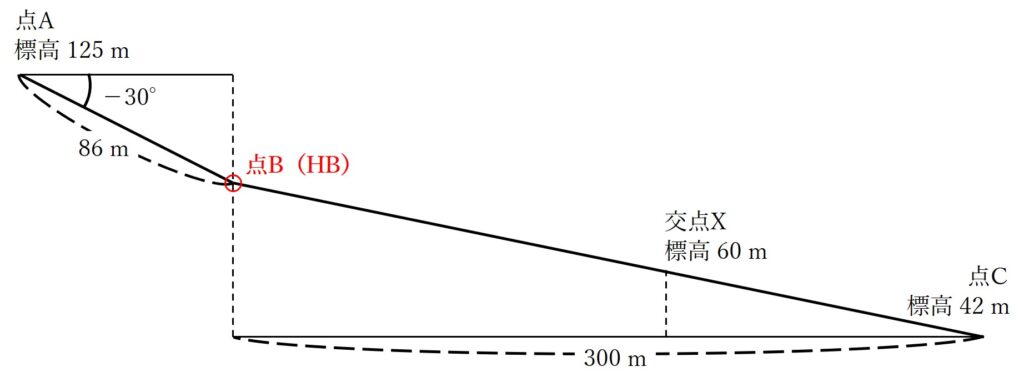
手順1 点Bの標高を求める
まずは、点Bの標高を求めていきます。点Bの標高はHBとします。
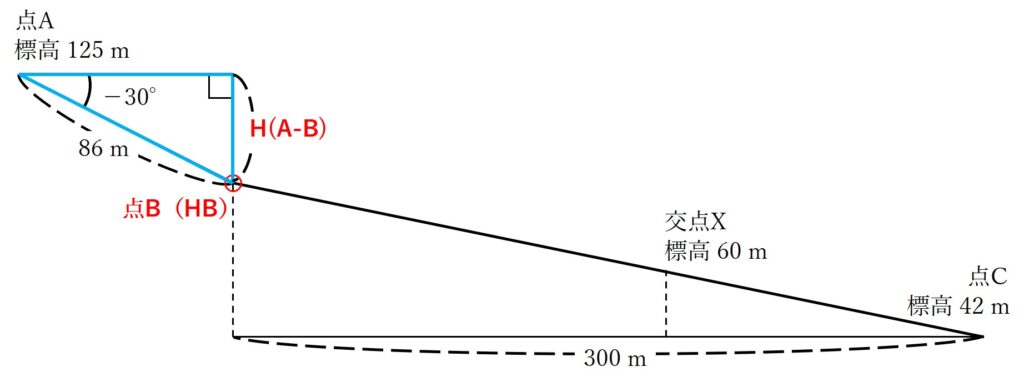
点Bの標高を求めるには、まずは1つの角度と1つの辺が分かっている上側の直角三角形を利用するといいですね。これは、点Aの標高から点Bの標高までの比高差を計算することで、点Bの標高を導き出すことができるからです。
今回はこの点Aの標高から点Bの標高までの差をH(A-B)とします。
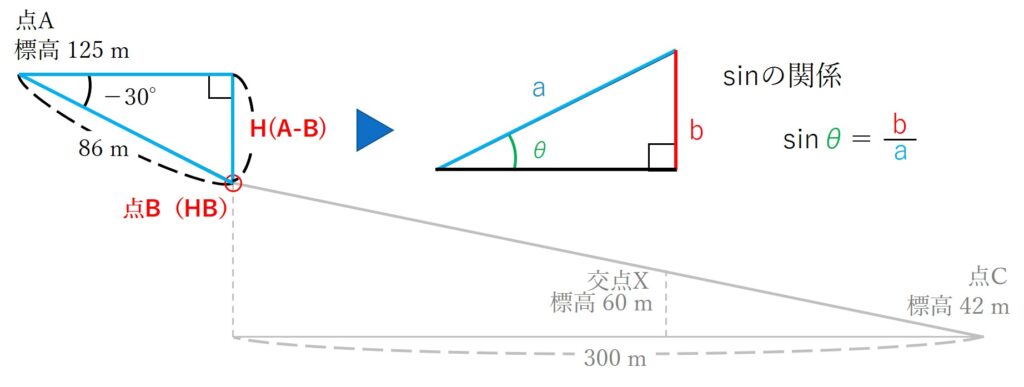
上側の直角三角形から、斜辺(点Aから点Bまでの距離)が86m・底辺と斜辺がなす角(点Aから点Bを見た高低角)が-30°とわかっていますので、三角関数のsinの関係を利用することでH(A-B)を計算することができそうです。
今回は、点Aと点Bの標高にどれだけの差があるかを確認したいので、計算しやすいように-30°は30°と置き換えます。
よって、三角関数のsinの関係から
sin(30°)=H(A-B)/86m
H(A-B)=sin(30°)×86m
関数表よりsin(30°)=0.5000なので
H(A-B)=0.5×86m=43m
となるので、点Aの標高から点Bの標高までの比高差はH(A-B)=43mとなります。
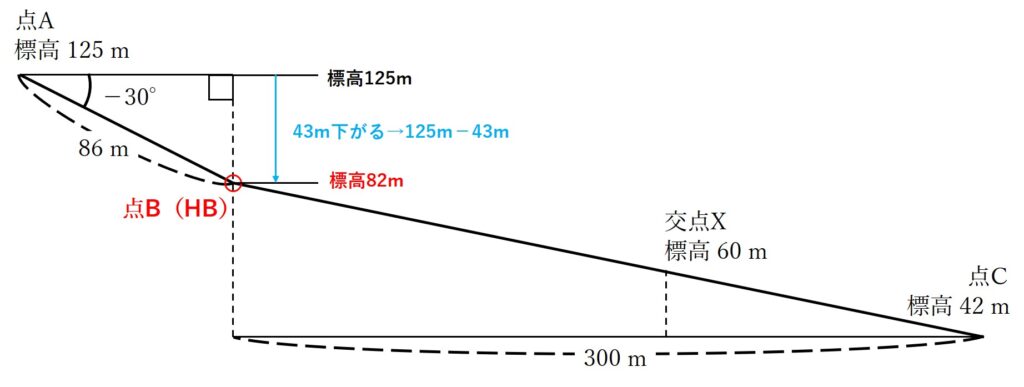
あとはこの差分、点Aの標高から引けば点Bの標高が求まりますので点Bの標高はHBは
HB=(点Aの標高)-(H(A-B))
=125m-43m
=82m
となります。
よって点Bの標高は82mです。
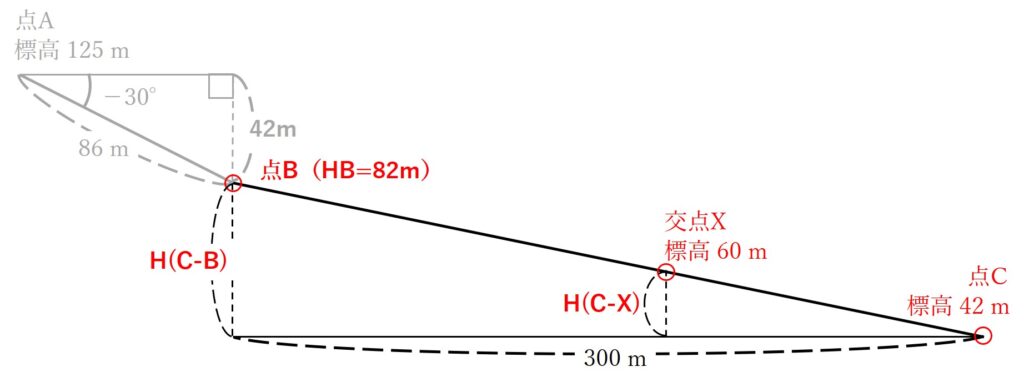
手順2 点Cと点B及び点Cと点Xの標高の差を求める
続いて、点Cと点Bの標高の差と点Cと点Xの標高の差を求めます。それぞれ点Cと点Bの標高の差をH(C-B)、点Cと点Xの標高の差をH(C-X)とします。
手順1で点Bの標高がわかりましたので点B、点C、点Xのそれぞれの標高は
- 点Bの標高=82m
- 点Cの標高=42m
- 点Xの標高=60m
とわかります。あとはそれぞれの標高の差を以下のように計算します。
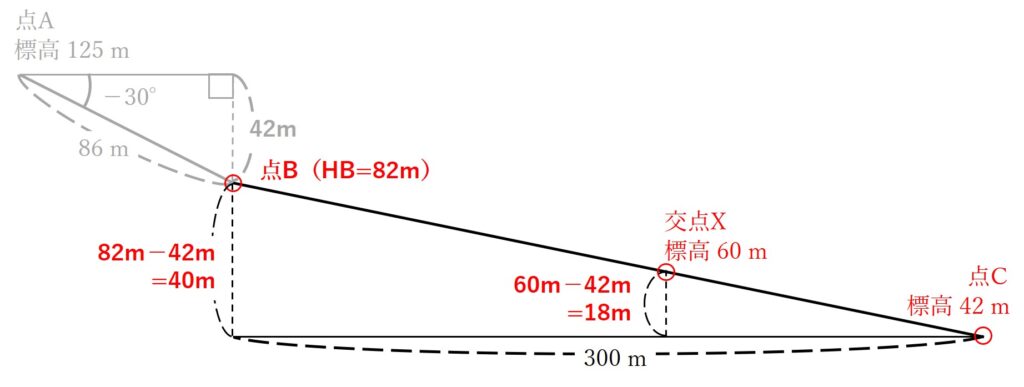
■点Cと点Bの標高の差(H(C-B))
H(C-B)=点Cの標高-点Bの標高
=42m-82m
=-40m
■点Cと点Xの比高差(H(C-X))
H(C-B)=点Cの標高-点Xの標高
=42m-60m
=-18m
よって、点Cと点Bの標高には40m、点Cと点Xの標高には18m、それぞれ差があることがわかりました。
手順3 点Cから点Xまでの距離Lを求める
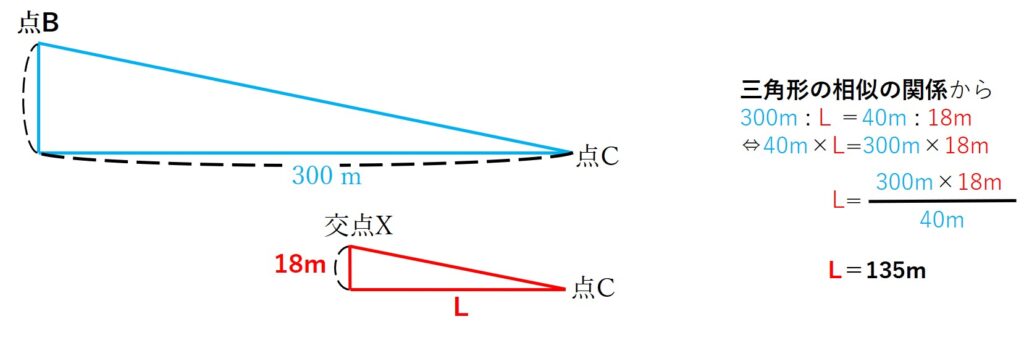
手順1~2で求めた内容を図にまとめると、以下のようになります。
図の中で青い三角と赤い三角は相似の関係です。(三角形の相似についてはコチラのページを参考にどうぞ。)
相似の三角形では以下のような関係が成り立ちますので、計算していきます。
結果、L=135.0mという結果を得ることができました。
手順4 1/500の地形図上のL(500)を求める
最後に、手順3で出した距離L=135.0mが、1/500の地形図上では何cmになるか計算していきます。
1/500の地形図は、私たちが生活しているこの空間を測った長さ(=1/1)を1/500倍(=0.002倍)小さくした長さが描かれたものです。
よって手順3で出した距離L=135.0mを1/500の地形図上で表現する場合は、距離Lを1/500倍してあげれば描くことができます。
よって、1/500の地形図上のLの数値L(500)は
L(500)=距離L×(1/500)
=135.0m×(1/500)
=0.27m
m(メートル)をcm(センチメートル)に直すには100倍すればよいので
0.27m×100=27cm
となります。よって、L(500)=27.0cmです。
上記結果に対応する選択肢は4となりますので、選択肢4が正解となります。
令和2年測量士補試験No.13のまとめ
「水準測量」からの出題でした。
本問は測量の問題として出ていますが、イメージは高校数学の計算問題に近いです。
数学が得意な人であれば簡単に解けると思います。数学が苦手な方は
- 三角関数
- 三角形の相似の計算
の2つをしっかりと習得していきましょう。
また、地形図の縮尺に関する考え方も大切です。
その他の測量士補試験の問題に挑戦!
令和2年のNO.13の問題を確認したら、その他の問題にも挑戦していきましょう!
本ブログでは各問題の解説を年度ごとに一覧にまとめたページがありますので、ぜひその記事からその他の問題に挑戦してみてください!
問題解説のまとめ記事はコチラからどうぞ!→過去問に挑戦!現役測量士の解説を読んで測量士補試験を攻略しよう!
さいごに
本ブログを参考にしていただきありがとうございます。
内容に関して不明な点、ご質問、指摘事項、感想などございましたら、コメントやメールにてご連絡ください。
励みになるとともに、本ブログをよりたくさんの皆様に有益なものにできると考えています。
ぜひお待ちしております。
お問い合わせ先:surveyor_kenzo☆aol.com
※ご連絡の際は☆を@に変更してください。

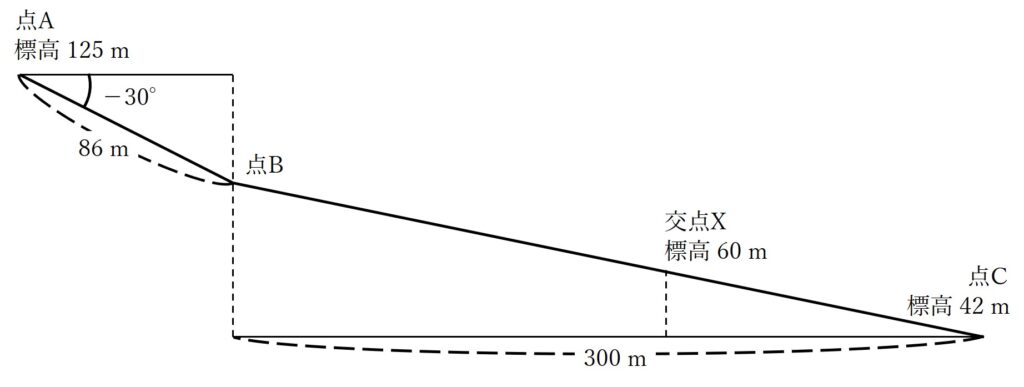 図14
図14