必要な用語や手法に関する解説も一緒におこなっていきますので、参考書代わりに本記事を使ってみてください。 その他の過去問の解説記事はコチラのリンクからどうぞ。
目次
令和2年測量士補試験No.27の問題文
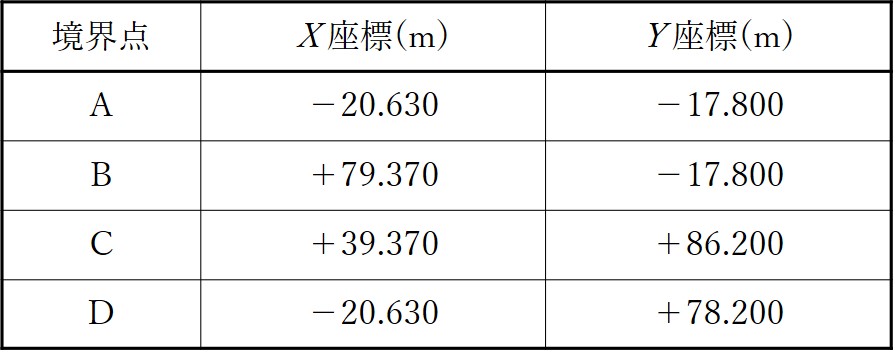
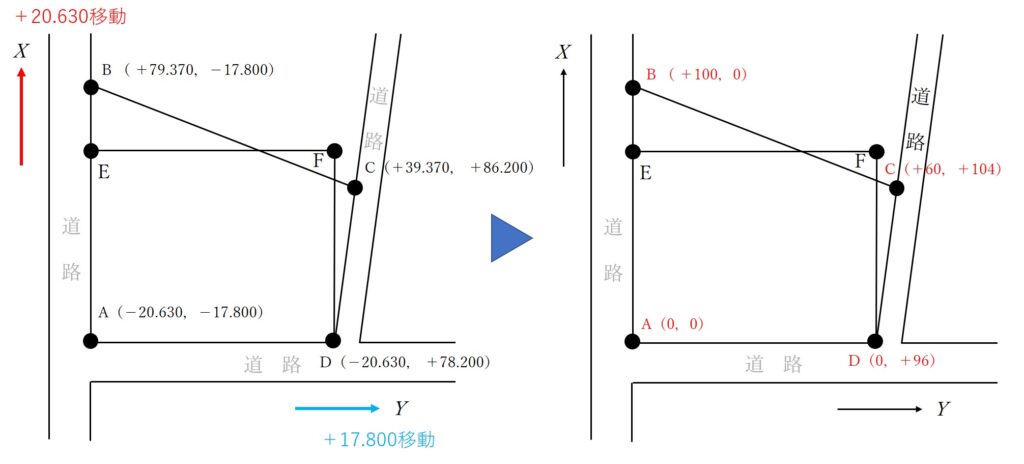
図27は,境界点A,B,C,Dの順に直線で結んだ土地を表したもので,土地を構成する各境界点の平面直角座標系(平成14年国土交通省告示第 9 号)に基づく座標値は表27のとおりである。
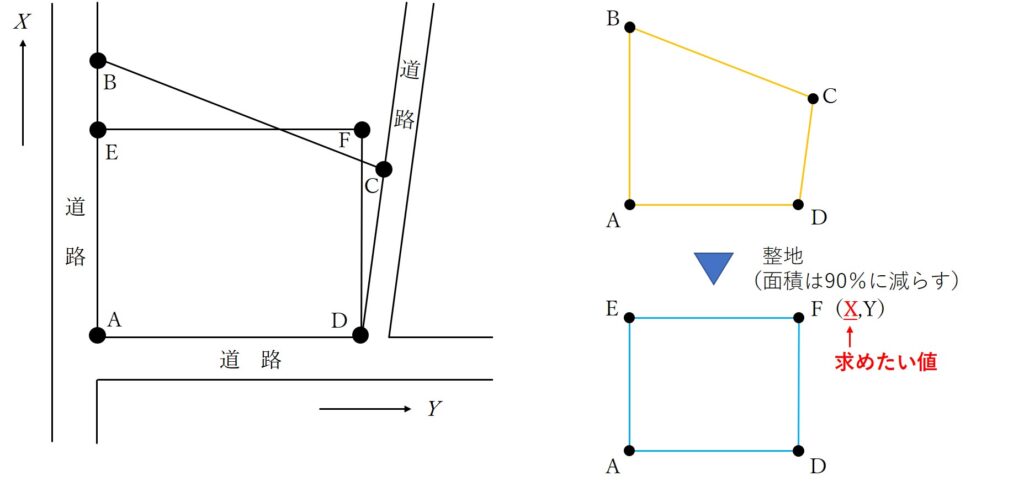
公共測量によって,土地ABCDの面積の90 %となる長方形AEFDに整えたい。このとき境界点FのX 座標値は幾らか。最も近いものを次の中から選べ。
なお,関数の値が必要な場合は,巻末の関数表を使用すること。
- +49.430
- +53.870
- +55.120
- +58.630
- +75.750
(令和2年測量士補試験問題集 No.27)
令和2年測量士補試験No.27の解答・解説
「応用測量」の分野からの出題です。
正解は「3」となります。
以下、解答を導くまでの詳しい計算の解説です。
計算に使用する関数表はコチラを参考にしてください。→関数表
境界点FのX 座標値を求める手順
まずは本問の内容を整理すると、以下のようになります。
- 土地ABCDを長方形AEFDにしたい
- 長方形AEFDの面積は土地ABCDの面積の90%
- 求めたいのは点FのX座標
点FのX座標を求めるためには長方形AEFDの面積が必要となり、長方形AEFDの面積を求めるためには土地ABCDの面積が必要となります。
また、土地ABCDの面積を求めるためには点Aの座標が(0,0)になるように図形を移動するという工夫も必要です。
よって、点FのX座標を求めるには以下の手順を踏んでいきます。
- 点Aの座標が(0,0)になるように図形を移動する
- 土地ABCDの面積を求める
- 長方形AEFDの面積を求める
- 点FのX座標を求める
少し手順が複雑そうですが、1つ1つ大事におこなえば解答までたどり着けます。
それぞれの手順の詳しい内容を見ていきましょう。
手順1 点Aの座標が(0,0)になるように図形を移動する
まずは、計算がしやすくなるように全体の座標を移動させます。
そのままでも計算はできるのですが、この作業をすると圧倒的に計算が楽になるのでなるべくおこないましょう。
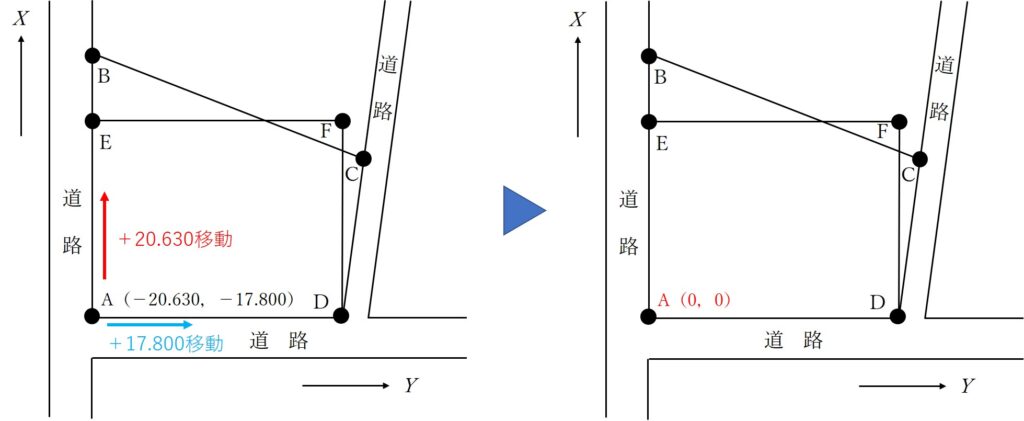
今回は点Aの位置が中心位置(座標原点)として利用しやすそうなので、点Aの位置が(0,0)になるように移動させます。
表27から点Aの現在の座標が(-20.630,-17.800)とわかるので、X座標に+20.630、Y座標に+17.800を足せば(0,0)になりますね。
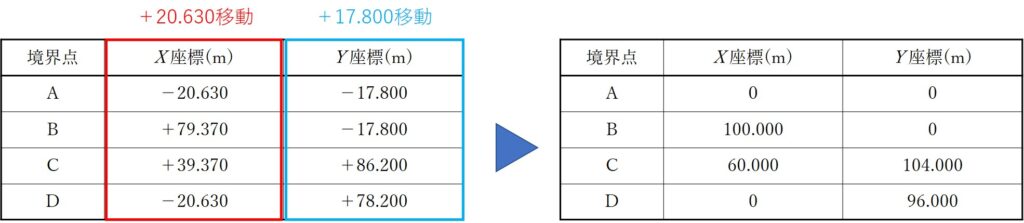
よって、すべての座標をX方向に+20.630、Y方向に+17.800移動させると全体の座標が動いたことになり、それぞれの座標は次の通りとなります。
移動後の各座標がキレイな数値になることからも、座標移動が前提の問題であることが分かります。
手順2 土地ABCDの面積を求める
続いて、土地ABCDの面積を求めていきます。
四角形がキレイな形(平行四辺形・台形・長方形など)をしていれば簡単に公式で求めることができるのですが、土地ABCDはそのような四角形ではありません。
このような時に使用するのが座標法という面積を求める方法です。
座標法では、まずは各位置に番号をつけます。どこの位置を最初にしても良いので、そこから時計回りに番号をつけていきましょう。
今回の場合は点Aを番号1として、そこから時計回りに
- 点A:番号1
- 点B:番号2
- 点C:番号3
- 点D:番号4
と番号をつけてみます。
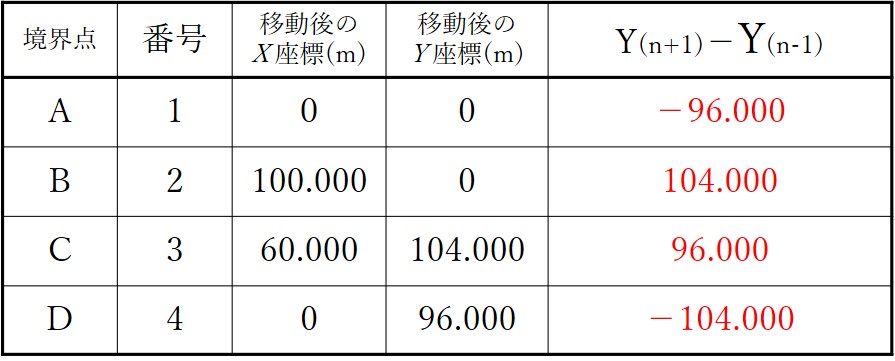
 続いて、各位置の前後の番号のY座標の差(Yn+1-Yn-1)を計算します。例えば、点Aは番号1なので「番号2(B)のY座標と番号4(D)のY座標の差」の計算が、点Bは番号2なので。「番号3(C)のY座標と番号1(A)のY座標の差」の計算が必要になります。
続いて、各位置の前後の番号のY座標の差(Yn+1-Yn-1)を計算します。例えば、点Aは番号1なので「番号2(B)のY座標と番号4(D)のY座標の差」の計算が、点Bは番号2なので。「番号3(C)のY座標と番号1(A)のY座標の差」の計算が必要になります。
整理が必要なので必ず以下のように表にまとめていきましょう。
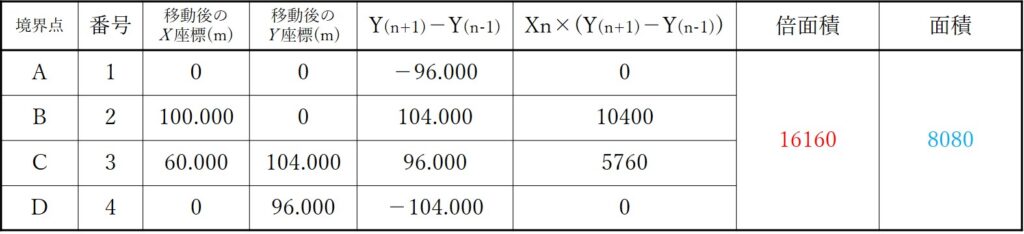
表の中身を計算すると、次のようになります。
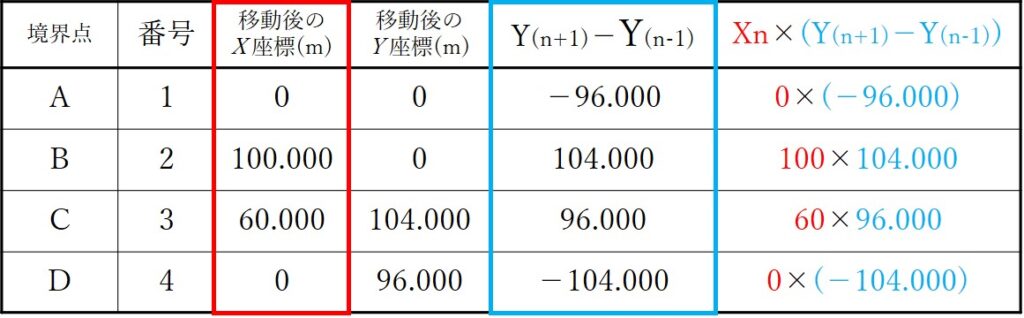
次に、上記計算結果に、X座標をかけます。計算は表の右につけたしておきましょう。
計算すると次のようになります。
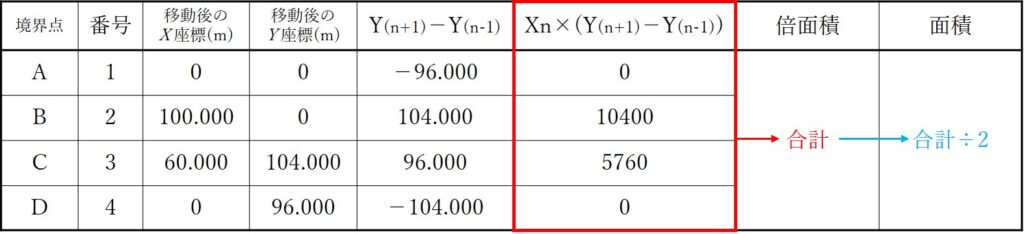
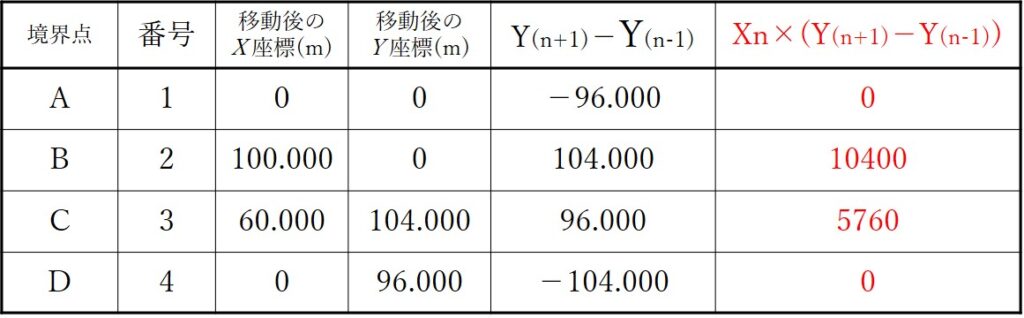 上記結果をすべてたすと、ABCDで囲まれた土地の面積の2倍の値が出てきます。
上記結果をすべてたすと、ABCDで囲まれた土地の面積の2倍の値が出てきます。
言い換えれば、上記結果をたした値を2で割ればABCDで囲まれた土地の面積が出るということです。
手順3 長方形AEFDの面積を求める
問題文から、長方形AEFDの面積は土地ABCDの面積の90%となることがわかっています。
つまり、手順2で計算した土地ABCDの面積を0.9倍すれば長方形AEFDの面積となります。
よって、長方形AEFDの面積は
長方形AEFDの面積=土地ABCDの面積×0.9
=8080㎡×0.9
=7272㎡
と計算できます。
以上のことから、長方形AEFDの面積は7272㎡となります。
手順4 点FのX座標を求める
最後に、点FのX座標を求めます。
長方形AEFDのうち地点AとDの座標がわかっています。
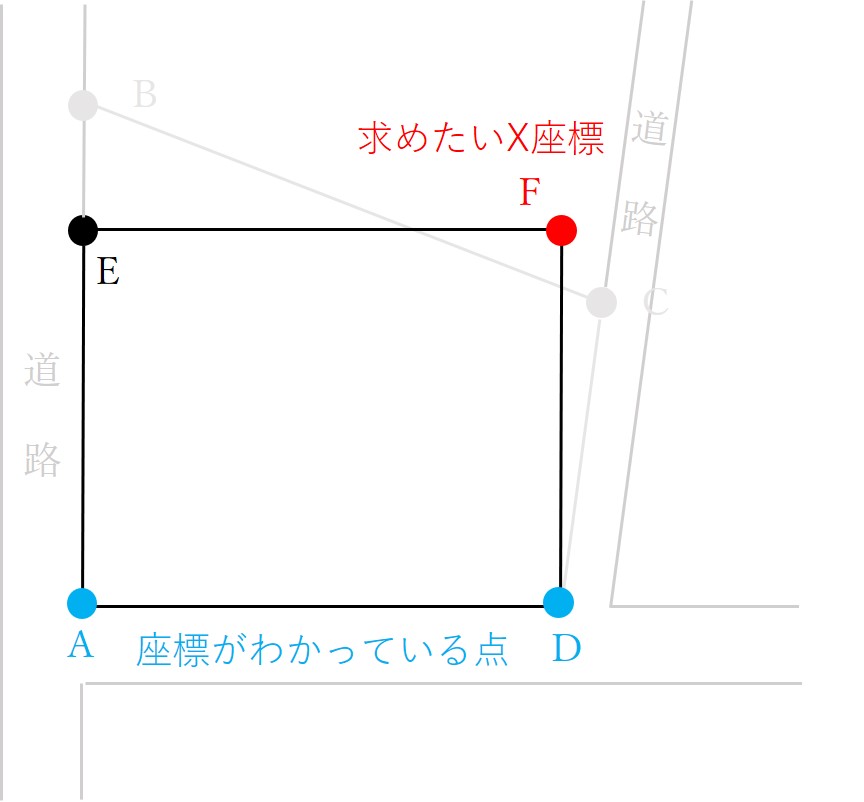 点Aと点Dの座標がわかっているということは、2つの点のY座標の差を計算すれば辺ADの長さを求められます。
点Aと点Dの座標がわかっているということは、2つの点のY座標の差を計算すれば辺ADの長さを求められます。
移動後の座標の方が計算しやすいのでその座標を用いると
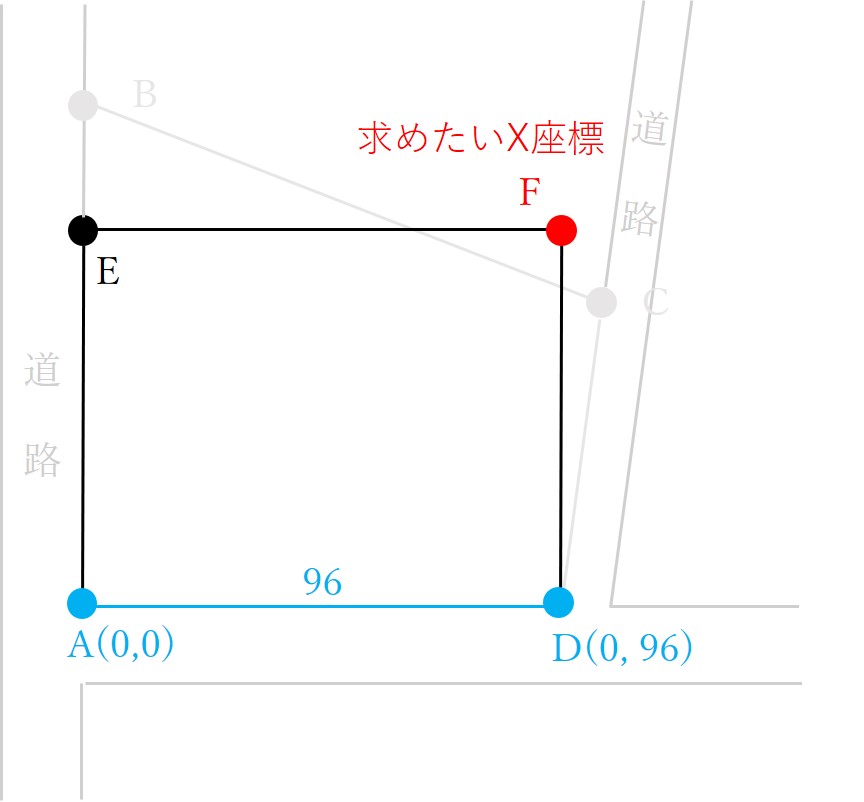
- AのY座標は0
- DのY座標は96
ですので、辺ADの長さは96となることがわかります。
 長方形の面積は縦×横で計算できるので、手順3で求めた長方形AEFDの面積=7272㎡、辺AD=96より
長方形の面積は縦×横で計算できるので、手順3で求めた長方形AEFDの面積=7272㎡、辺AD=96より
長方形AEFDの面積=縦×横
7272=縦×96
縦=7272÷96
=75.75
と計算できます。
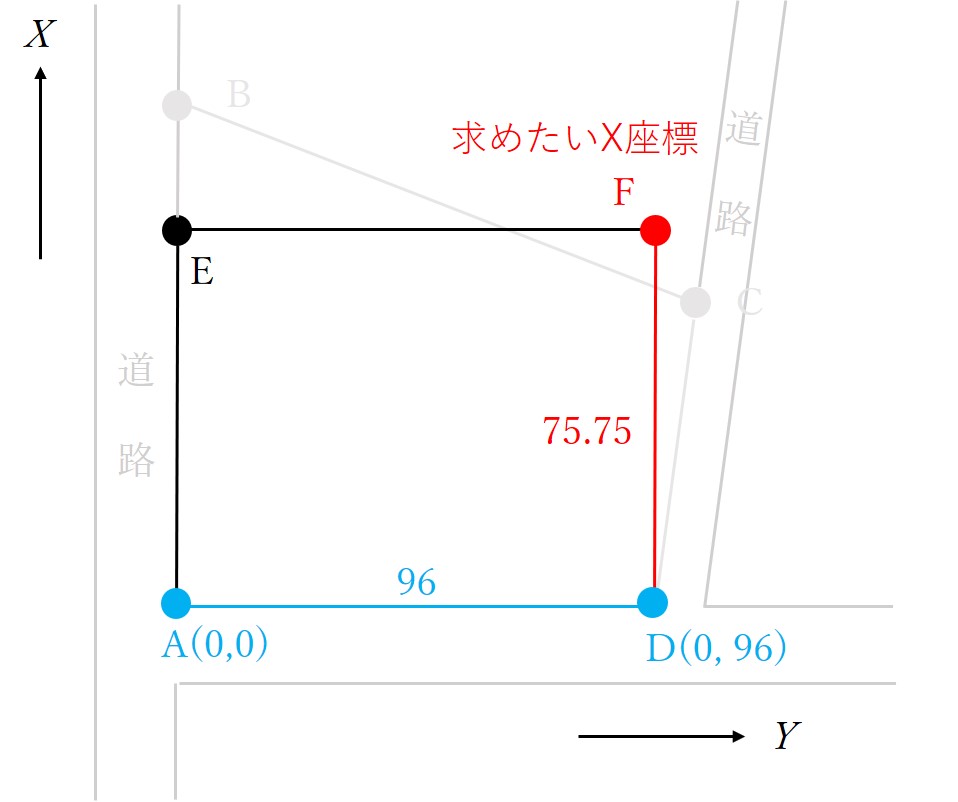
縦の長さが75.75とわかれば、あとはDのX座標にその数値をたせば、Fの座標ということです。
ここまでの計算は移動後の座標を用いてるので注意してください。
さいごに、元の座標で計算を行います。
Dの元々のX座標は-20.630なので、それに75.75をたすと
FのX座標=DのX座標+75.75
=-20.630+75.75
=55.120
よって、FのX座標は55.120となります。
上記数値に対応する選択肢の番号は「3」となりますので、正しい選択肢は「3」と言えます。
令和2年測量士補試験No.27のまとめ
応用測量の分野からの出題でした。
座標法を用いた面積計算がキモとなる問題です。
座標法の考え方はたまにでる内容ですが、苦手なかたは後回しにしても良い内容だと思います。
何回か解いて感覚だけはしっかりとつかんでおきましょう!
令和2年測量士補試験No.26の類題
他年度の測量士補試験に出題された本問の類題です!ぜひチャレンジしてみてください!
令和3年測量士補試験問題集NO.27→問題文及び解説記事はコチラ
令和4年測量士補試験問題集NO.27→問題文及び解説記事はコチラ
その他の測量士補試験の問題に挑戦!
令和2年のNO.27の問題を確認したら、その他の問題にも挑戦していきましょう!
本ブログでは各問題の解説を年度ごとに一覧にまとめたページがありますので、ぜひその記事からその他の問題に挑戦してみてください!
問題解説のまとめ記事はコチラからどうぞ!→【令和5年】問題解説リンク集から現役測量士の解説を読んで測量士補試験の過去問を攻略しよう!!
さいごに
本ブログを参考にしていただきありがとうございます。
内容に関して不明な点、ご質問、指摘事項、感想などございましたら、コメントやメールにてご連絡ください。
励みになるとともに、本ブログをよりたくさんの皆様に有益なものにできると考えています。
ぜひお待ちしております。
お問い合わせ先:surveyor_kenzo☆aol.com
※ご連絡の際は☆を@に変更してください。

 図27
図27