必要な用語や手法に関する解説も一緒におこなっていきますので、参考書代わりに本記事を使ってみてください！
目次
令和２年測量士補試験No.１１の問題文
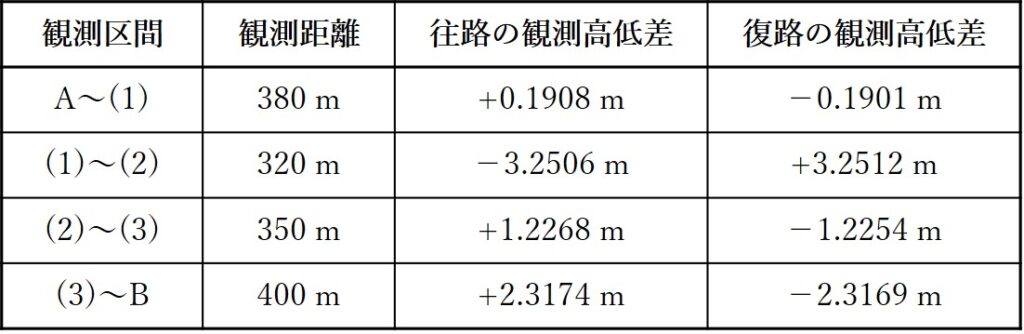
図11は，水準点Aから固定点（1），（2）及び（3）を経由する水準点Bまでの路線を示したものである。この路線で 1 級水準測量を行い，表11に示す観測結果を得た。再測すべき観測区間はどれか。次の中から選べ。
ただし，往復観測値の較差の許容範囲は，S を観測距離（片道，km単位）としたとき，2.5 mm√S とする。
なお，関数の値が必要な場合は，巻末の関数表を使用すること。
- A～(１)
- (１)～(２)
- (２)～(３)
- (３)～B
- 再測の必要はない
（令和2年測量士補試験問題集 No.11）
図11
令和２年測量士補試験No.１１の解答・解説
「水準測量」の分野からの出題です。
解答は「３」となります。以下、詳しい計算方法と解説です。
計算に使用する関数表はコチラを参考にしてください。→関数表
水準測量の再測の有無の確認のルール
水準測量の再測については国土地理院の定める作業規程の準則の第2編第3章第5節第65条でルールが定められています。
第６５条（再測）
１級水準測量、２級水準測量、３級水準測量及び４級水準測量の観測において、水準点及び個定点によって区分された区間の往復観測値の較差が、許容範囲を超えた場合は、再測するものとする。
一 往復観測値の較差の許容範囲は、次表を標準とする。
二 １級水準測量及び２級水準測量の再測は、同方向の観測値を採用しないものとする。
（作業規程の準則 P34）
この条文にあるルールを要約すると、再測が必要な区間を確認するためには以下の作業をおこなう必要があります。
- 水準点間の区間の往復観測の較差を確認する
- 各水準点間及び固定点の区間の往復観測の較差を確認する
- それぞれの較差が許容範囲内か確認する
また、問題文にもありますが1級水準測量の往復観測の較差は「2.5mm√S」で求めます。
また、条文にはないですが、計算結果の読定値の小数点以下は切り捨てするというルールもあります。
再測すべき観測区間を求めるまでの手順
作業規程の準則のルールにのっとりながら、今回の問題を解いていくと次のような手順になります。
- 表11にA～Bの区間を追加する
- 各区間の観測高低差の往復の較差を計算する
- 較差が許容範囲内か確認する
次の章から、それぞれの手順の詳しい内容を見ていきましょう！
手順１ 表11にA~Bの区間を追加する
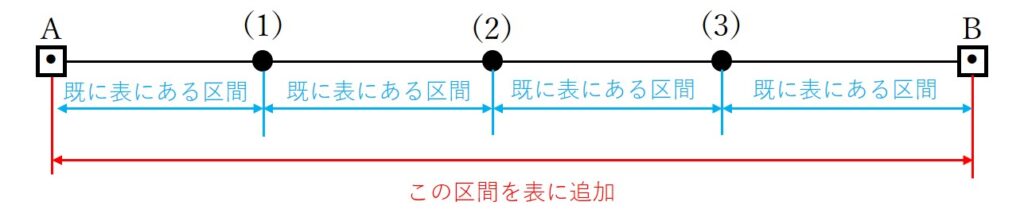
本問では表11に記載がある各区間以外に、A～Bの水準点の区間の較差も確認する必要があります。
それをわかりやすくするために、まずは表11の一番下にA~Bの行を追加していきましょう！
続いて、観測距離、往路の観測高低差、復路の観測高低差のそれぞれの数値を埋めていきます。
それぞれの数値は、表の各区間の数値を全てたしていけば大丈夫です！
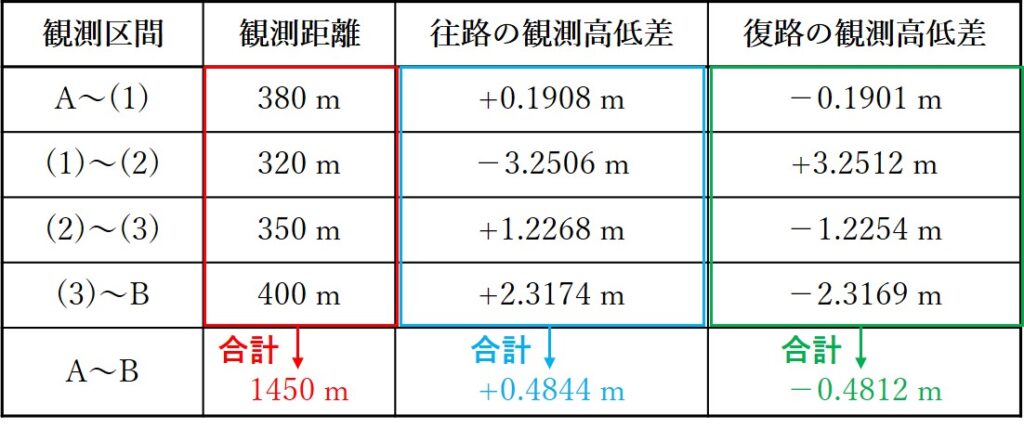これで、表11にA~Bの行の追加が完了しました！続いて較差を求めていきましょう！
手順２ 各区間の観測高低差の往復の較差を計算する
再測区間を特定するためには、手順１で作成した表を利用して「観測高低差の往復の較差」を計算する必要があります。
往復の較差を計算するので、「往路の観測高低差－復路の観測高低差」を各区間で行えば大丈夫です。
各区間を計算して、手順１で作成した表に追加しちゃいましょう。
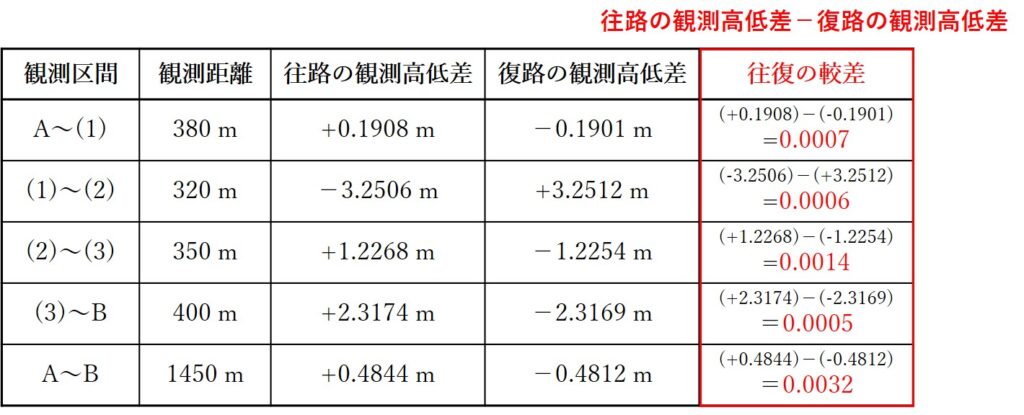これで各区間の往復の較差を計算できたので、次の手順でそれぞれの較差の数値が許容範囲内か確認していきます！
確認の仕方は次の手順で見ていきましょう！
手順３ それぞれの較差が許容範囲内か確認する
較差許容範囲の数値は問題文より次の式を利用することが書かれています。
- 2.5 mm√S（Sは観測距離（片道，km単位））
よって、それぞれの区間の較差の許容範囲は次のように計算できます。
A~(1)（観測距離380m＝0.38km）
許容範囲＝2.5mm×√0.38
ここで、√0.38＝√0.01×√38とすると
√0.01＝0.1，関数表より√38＝6.16441なので
許容範囲＝2.5mm×√0.38
＝2.5mm×(√0.01×√38)
＝2.5mm×(0.1×6.16441)
＝2.5mm×0.616441
≒1.5411mm
＝0.0015441m
≒0.0015m（少数第5位以下は切り捨て）
(1)~(2)（観測距離320m＝0.32km）
許容範囲＝2.5mm×√0.32
ここで、√0.32＝√0.01×√32とすると
√0.01＝0.1，関数表より√32＝5.65685なので
許容範囲＝2.5mm×√0.32
＝2.5mm×(√0.01×√32)
＝2.5mm×(0.1×5.65685)
＝2.5mm×0.565685
≒1.4142mm
＝0.0014142m
≒0.0014m（少数第5位以下は切り捨て）
(2)~(3)（観測距離350m＝0.35km）
許容範囲＝2.5mm×√0.35
ここで、√0.35＝√0.01×√35とすると
√0.01＝0.1，関数表より√35＝5.91608なので
許容範囲＝2.5mm×√0.35
＝2.5mm×(√0.01×√35)
＝2.5mm×(0.1×5.91608)
＝2.5mm×0.591608
≒1.4790mm
＝0.0014790m
≒0.0014m（少数第5位以下は切り捨て）
(3)~B（観測距離400m＝0.40km）
許容範囲＝2.5mm×√0.40
ここで、√0.35＝√0.01×√40とすると
√0.01＝0.1，関数表より√40＝6.32456なので
許容範囲＝2.5mm×√0.40
＝2.5mm×(√0.01×√40)
＝2.5mm×(0.1×6.324568)
＝2.5mm×0.6324568
≒1.5811mm
＝0.0015811m
≒0.0015m（少数第5位以下は切り捨て）
A~B（観測距離1450m＝1.45km）
許容範囲＝2.5mm×√1.45
ここで、√1.45＝√0.01×√5×√29とすると
√0.01＝0.1，関数表より√5＝2.23607，√29=5.38516なので
許容範囲＝2.5mm×√1.45
＝2.5mm×(√0.01×√5×√29)
＝2.5mm×(0.1×2.23607×5.38516)
＝2.5mm×1.2041594721
≒3.0104
＝0.003014m
≒0.0030m（少数第5位以下は切り捨て）
以上のことを手順２で作成した表に付け加えると、次のようになります。
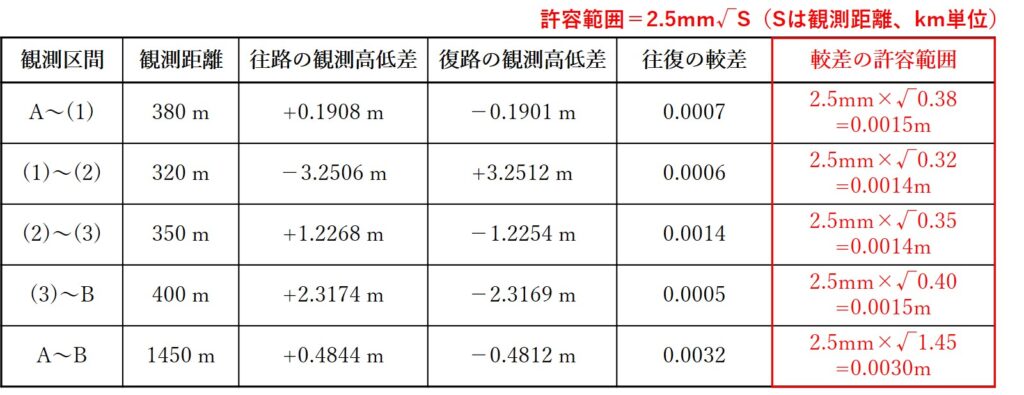あとはそれぞれの区間の「往復の較差の数値」と「許容範囲」を見比べて、許容範囲内の数値をクリアしているか確認していきます。それぞれの区間を確認してみると
となります。
A~Bの水準点区間は不合格、(2)～(3)はギリギリセーフ…といった感じですね。
よってA~B全体を再測！とはなりませんので安心してください笑
このようなときは、最も数値的に改善の余地がある区間を再測するのが鉄則です。
今回であればギリギリ合格ラインの(2)～(3)がまだまだ数値的に良い結果を出せそうなので、(2)～(3)の区間を再測するのがよさそうです。
よって、本問の正解は(2)～(3)の区間である選択肢３となります。
令和２年測量士補試験No.１１のまとめ
「水準測量」からの出題でした。
水準測量の較差に関する計算は、頻出ではないですがたまに出る問題です。
計算に時間がかかる可能性があるので、苦手な人は捨てるのも1つの手だと思います。
余裕のある人は何度も解いて問題に慣れておきましょう！
その他の測量士補試験の問題に挑戦！
令和2年のNO.11の問題を確認したら、その他の問題にも挑戦していきましょう！
本ブログでは各問題の解説を年度ごとに一覧にまとめたページがありますので、ぜひその記事からその他の問題に挑戦してみてください！
問題解説のまとめ記事はコチラからどうぞ！→過去問に挑戦！現役測量士の解説を読んで測量士補試験を攻略しよう！
さいごに
本ブログを参考にしていただきありがとうございます。
内容に関して不明な点、ご質問、指摘事項、感想などございましたら、コメントやメールにてご連絡ください。
励みになるとともに、本ブログをよりたくさんの皆様に有益なものにできると考えています。
ぜひお待ちしております。
お問い合わせ先：surveyor_kenzo☆aol.com
※ご連絡の際は☆を@に変更してください。