必要な用語や手法に関する解説も一緒におこなっていきますので、参考書代わりに本記事を使ってみてください。
目次
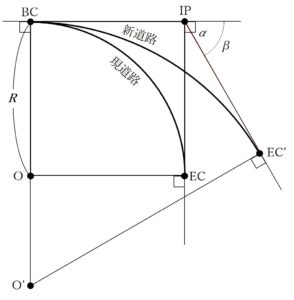
令和４年測量士補試験No.２５の問題文
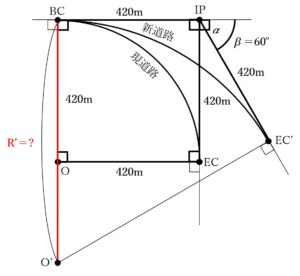
図 25 に示すように，曲線半径 R = 420 m，交角 α = 90°で設置されている，点 O を中心とする円曲線から成る現在の道路（以下「現道路」という。）を改良し，点 O’ を中心とする円曲線から成る新しい道路（以下「新道路」という。）を建設することとなった。
新道路の交角 β = 60°としたとき，新道路 BC ～ EC’ の路線長は幾らか。最も近いものを次の中から選べ。
ただし，新道路の起点 BC 及び交点 IP の位置は，現道路と変わらないものとし，円周率π = 3.14 とする。
なお，関数の値が必要な場合は，巻末の関数表を使用すること。
図25
- 440 m
- 659 m
- 727 m
- 743 m
- 761 m
（令和4年測量士補試験問題集 No２５）
令和４年測量士補試験No.２５の解答・解説
「応用測量」の分野からの出題です。
正解は「５」となります。
以下、計算手順の詳しい解説です。
計算に使用する関数表はコチラを参考にしてください。→関数表
新道路BC～EC’ の路線長を導くまでの計算手順
新道路BC～EC' の路線長を導くまでには、以下の手順を踏んでいく必要があります。
- 問題文からわかる範囲で図に示していく
- 共通の交点IPを持つ円曲線の性質を利用してO' ～BCの距離を求める
- 新道路BC～EC' の路線長を求める
今回の問題で特に重要なのは手順２の項目で、公式を知っているかどうかでこの問題を素早く解けるかどうかが決まります。
1つ1つ手順を理解していき、覚えるべき公式をきちんと押さえていきましょう！
手順１ 問題文からわかる範囲で図に示していく
最初は、問題文からわかることを図に書き込んでいきましょう！
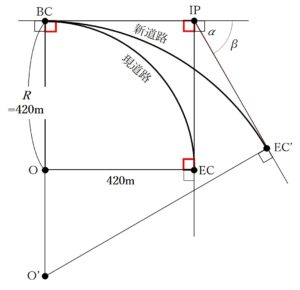
現道路の曲線半径Rは420mです。現道路はOを中心とした円の一部なので、その半径にあたる「BC～O」と「EC～O」は420mということになります。
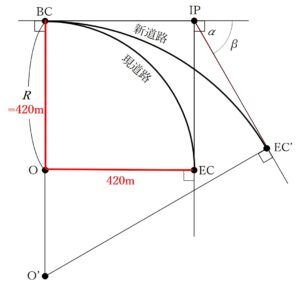さらに、IPがBCとECからの交点なので∠O-BC-IP＝90°、∠O-EC-IP=90°、問題文から∠α＝90°なのでその隣の∠BC-IP-EC＝90°となります。
加えて、四角形の内角の和は360°ですので、
∠BC-O-EC＝360°－（∠O-BC-IP）－（∠O-EC-IP）－（∠BC-IP-EC＝90°）
∠BC-O-EC＝360°－90°－90°－90°
∠BC-O-EC＝90°
となりますから、BC～O＝EC～O＝420mの条件も加えて、四角形BC－O－EC－IPは正方形であることがわかり、BC～IPおよびEC～IPは
BC～IP＝EC～IP＝420mであることがわかります。
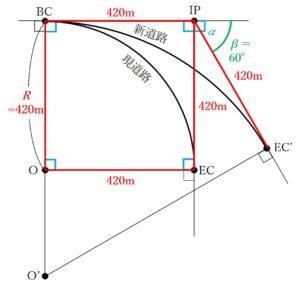
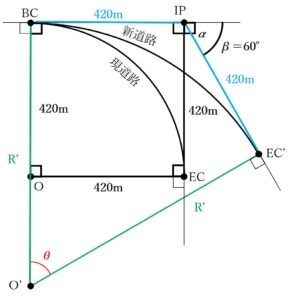
さらに、円曲線の交点からそれぞれの接点までの長さは同じですので、O' を中心に持つ円曲線である新道路のBC～IPとEC' ～IPの長さは
BC～IP＝EC´ ～IP＝420m
であることもわかります。
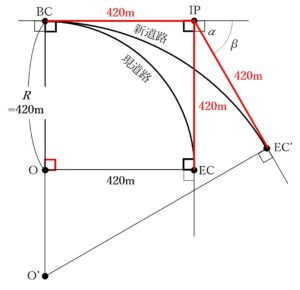最後に、問題文から∠β＝60°であることがわかっていますので、これまでの説明をすべてまとめて書き込むと、次のようになります。
手順２ 共通の交点IPを持つ円曲線の性質を利用してO' ～BCの距離を求める
円曲線の長さは、
- 円曲線の半径
- 交角
の2つが分かっていれば求めることができます。
今回求めたいのは「新道路BC～EC' の路線長」なので、BC～EC' の円曲線の「半径」と「交角」が分かっていれば求めることができそうです。
問題文から「交角β＝60°」であることはわかっているのですが、BC～EC' の円曲線の半径O´ －BCの長さがわかりません…。
そのためこの手順で、半径O´ －BCの長さを求めていきます。また、この手順では半径O´ －BCの長さを「R´」とします。
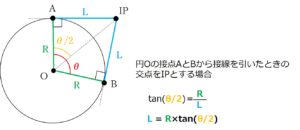
R´の長さを求める考え方ですが、中心Oの円曲線があり、その円曲線から2つの接線が交わった点（交点）がある場合、次のような関係が成り立ちます。
今回の問題に当てはめると、次のような関係になりますね。
「これじゃあθが分からないのでは？？」と思う方がいるかもしれませんが、実は円には「交角＝中心角」という性質があります。つまり、∠θ＝∠β＝60°となるのです！
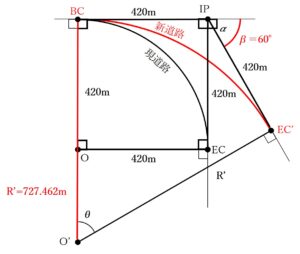
以上のことからＲ´ を求めるための条件が出そろいましたので計算すると、
となるので、R´ ＝727.462となります。
手順３ 新道路BC～EC' の路線長を求める
手順２の説明でも出ていますが、「新道路BC～EC' の路線長」なので、BC～EC' の円曲線の「半径」と「交角」が分かっていれば求めることができます。
上図の計算式に当てはめれば、
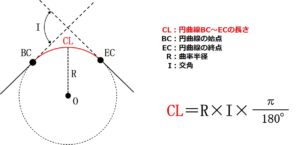
- CL=新道路BC～EC' の路線長
- R=R'=727.462
- I＝β＝60°
となります。
計算していくと
CL＝R×I×(π/180°)
CL＝727.462×60°×(π/180°)
＝727.462×π×(60°/180°)
＝727.462×π×(1/3)
問題文より円周率π = 3.14なので
CL=727.462×3.14×(1/3)
＝761.410
よって、CL=新道路BC～EC' の路線長＝761.410となりました。
最も近しい選択肢の数字は選択肢５の761mとなるので、選択肢５が正解となります。
令和４年測量士補試験No.２５のまとめ
応用測量の分野からの出題でした。
応用測量のうち、共通の交点を持つ旧道路と新道路があった場合の新道路の円曲線の延長を求める問題です。
この問題のポイントは
- 円曲線の長さの計算
- 接点から交点の長さと半径の長さと中心角の関係
- 交角＝中心角
の3つです。
攻略できるようにしっかりと公式を覚えておきましょう！
令和４年測量士補試験No.２５の類題
他年度の測量士補試験に出題された本問の類題です！ぜひチャレンジしてみてください！
令和2年測量士補試験問題集NO.26→問題文及び解説記事はコチラ
令和3年測量士補試験問題集NO.26→問題文及び解説記事はコチラ
その他の測量士補試験の問題に挑戦！
令和4年のNO.25の問題を確認したら、その他の問題にも挑戦していきましょう！
本ブログでは各問題の解説を年度ごとに一覧にまとめたページがありますので、ぜひその記事からその他の問題に挑戦してみてください！
問題解説のまとめ記事はコチラからどうぞ！→過去問に挑戦！現役測量士の解説を読んで測量士補試験を攻略しよう！
さいごに
本ブログを参考にしていただきありがとうございます。
内容に関して不明な点、ご質問、指摘事項、感想などございましたら、コメントやメールにてご連絡ください。
励みになるとともに、本ブログをよりたくさんの皆様に有益なものにできると考えています。
ぜひお待ちしております。
お問い合わせ先：surveyor_kenzo☆aol.com
※ご連絡の際は☆を@に変更してください。