必要な用語や手法に関する解説も一緒におこなっていきますので、参考書代わりに本記事を使ってみてください！
目次
令和２年測量士補試験No.７の問題文
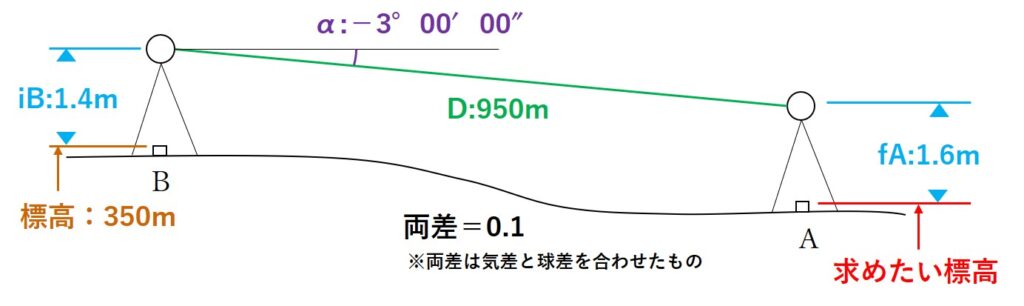
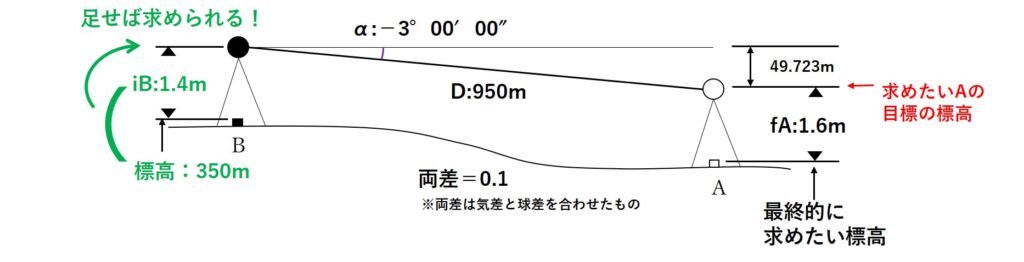
図7 に示すとおり，新点Aの標高を求めるため，既知点Bから新点Aに対して高低角α及び斜距離Dの観測を行い，表 7 の結果を得た。新点Aの標高は幾らか。最も近いものを次の中から選べ。
ただし，既知点Bの器械高iBは1.40 m，新点Aの目標高fAは1.60 m，既知点Bの標高は350.00 m，両差は0.10 mとする。また，斜距離Dは気象補正，器械定数補正及び反射鏡定数補正が行われているものとする。
なお，関数の値が必要な場合は，巻末の関数表を使用すること。
図7
- 297.38 m
- 300.08 m
- 300.18 m
- 300.38 m
- 303.38 m
（令和2年測量士補試験問題集 No.7）
令和２年測量士補試験No.７の解答・解説
「多角測量」の分野からの出題です。
解答は「３」です。以下、解答を導く計算の詳しい解説です。
計算に使用する関数表はコチラを参考にしてください。→関数表
新点Aの標高を導くための計算手順
本問は、高さが分かっている新点Bから新点Aを見たときの斜距離と角度が分かったうえで、新点Aの標高を求める問題です。
新点Aを求めるには、以下の手順を踏む必要があります。
- 問題文からわかる情報を図にまとめる
- 新点Aの高さを計算する
計算する方法さえわかっていれば、図にまとめるだけで解きやすくなる問題です。
それぞれの手順を詳しく見ていきましょう！
手順１ 問題文からわかる情報を図にまとめる
まずは、問題文からわかる情報をまとめていきましょう！
問題文と表７から以下のことがわかります。
- Bの機械高iB＝1.40m
- Aの目標高fB=1.60m
- Bの標高＝350m
- 両差＝0.10m
- B→Aの高低角＝－3°00′00″
- 斜距離Ｄ＝950.00m
以上の情報を図にまとめると図のようになりますね。
両差とは
両差は、気差（光の屈折による誤差）と球差（地球が丸いことによる誤差）を合わせた誤差です。
両差が0.1mということは観測した結果に0.1mの誤差が発生しているということなので、観測結果を補正しなければなりません。
既知点（B）から未知点（A）を観測するときは＋、未知点（A）から既知点（B）を観測するときは－として計算します。
実際に問題で計算してみましょう！
手順２ 新点Aの高さを計算する
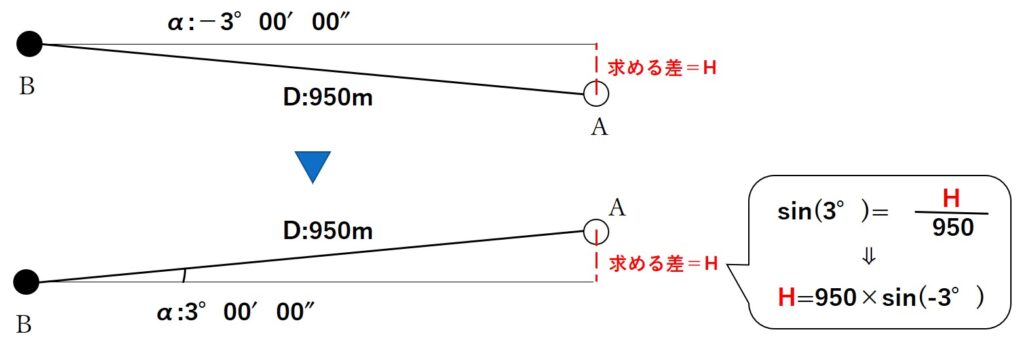
新点Aの高さを計算するには、Bに設置した機械までの標高とAに設置した目標の位置までの標高にどのぐらい差があるかを求める必要があります。
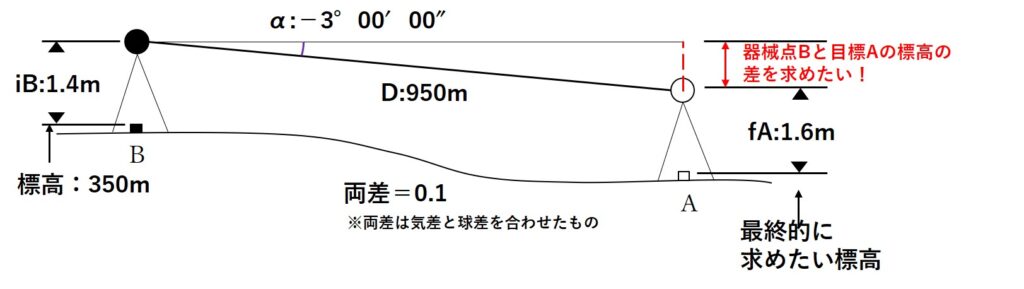本問では、B地点の器械からA地点の目標を見たときの高低角－３°と斜距離D＝950mが分かっています。
この2つが分かっているので、sinの関係を使えば求めたい標高の差を求めることができそうですね。
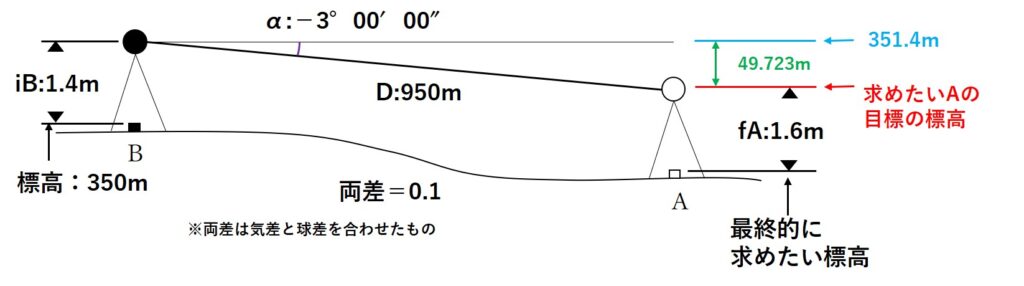
よって標高の差Hは
H=sin(3°)×950m
関数表よりsin(3°)＝0.05234なので
H=0.05234×950m＝49.723m
となります。
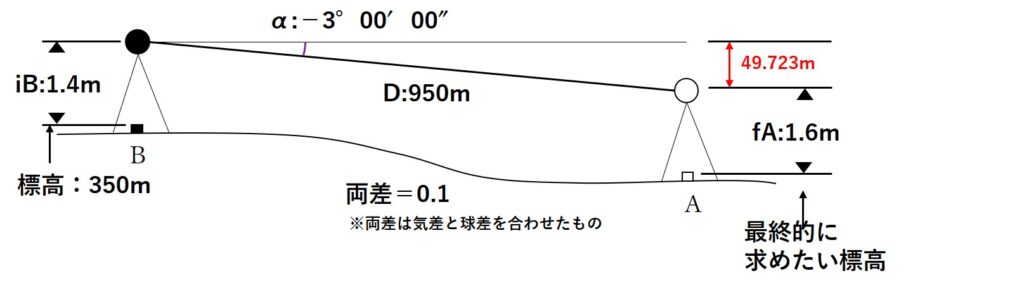
Bに設置した機械までの標高とAに設置した目標の位置までの標高の差がわかったので、続いてAに設置した目標の標高を求めましょう！
Aに設置した目標の標高は、Bに設置した機械までの標高がわかれば、先ほど計算したHの値を利用して求めることができそうです。
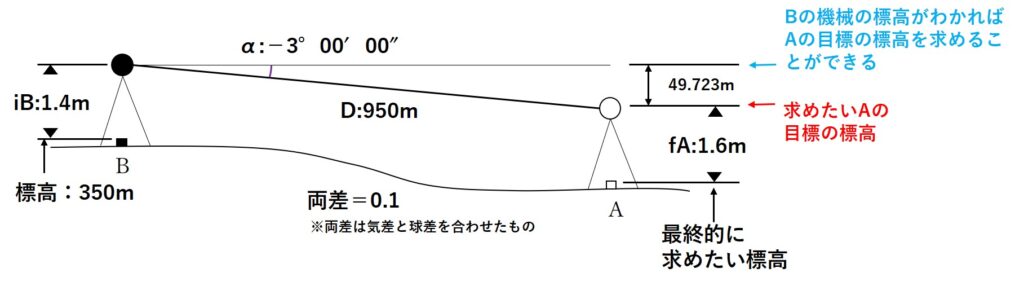
そのため、まずはBに設置した器械の標高を求めます。
- Bの標高は350m
- Bの機械高iB＝1.40m
がわかっているので、Bの標高にBの機械高を足せば機械の標高を出すことができます。
よってBの機械の標高Hbとすると、
Hb＝Bの標高+Bの機械高
＝350m＋1.40m
＝351.4m
と出すことができます。
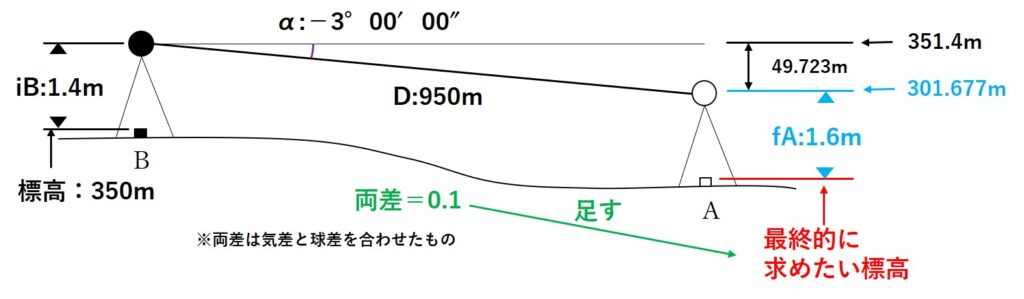
あとは、Bの機械の標高Hbから先ほど計算したAとBの差であるHを引いてあげれば、Aの目標の標高を求めることができそうです。
よってAの目標の標高をHaとすると、
Ha＝Bの機械の標高Hb－AとBの差H
＝351.4－49.723
＝301.677
となります。
ここまできたら、後はAの目標の標高HaからAの目標高faをひいてあげればAの標高HAが出そうですね…と言いたいところですが最後に忘れてはいけない要素があります。
それは両差です！両差の値を足すか引くかは観測の方向によって変わりますが、今回は既知点（B）から未知点（A）を観測するパターンなので足す必要があります。
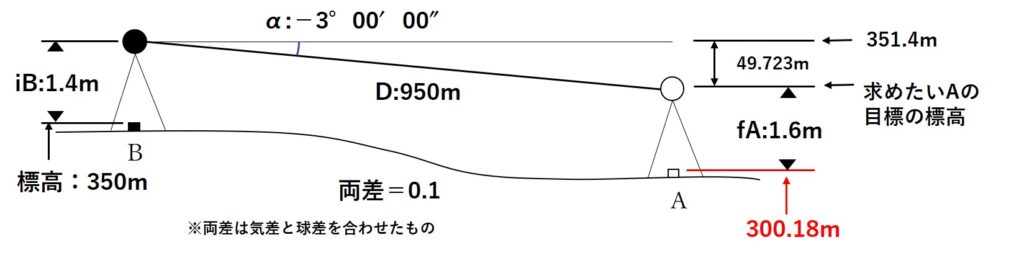
よって、Aの標高HAは
Aの標高HA=Aの目標高の標高Ha－Aの目標高fA＋両差
＝301.677－1.6＋0.1
＝300.177
≒300.18
となります。
よって新点Aの標高＝300.18なので、正解の選択肢は「３」となります。
令和２年測量士補試験No.７のまとめ
「多角測量」の分野からの出題でした。
今回のように新点の標高を求める際のポイントは
- 計算を順序だててできるか
- 両差を足すか引くか判断できるか
の2つです。
計算に関しては最初は順序だてて計算できるようにして、慣れてきたら
HA=（350m＋1.4m）－（sin(3°)×950m）－1.6m＋0.1m
のように計算するといいです！初めからこの式を無理やり作ろうとすると計算間違いを起こしてしまいます。
また、両差については
- 既知点（B）から未知点（A）を観測するときは＋
- 未知点（A）から既知点（B）を観測するときは－
で計算することをおさえて、正しい回答を導けるようにしておきましょう。ここで間違えると、選択肢を誤ってしまいます。
さいごに
さべろぐでは、測量士補試験合格を目指す人を応援しています！
受験に関する相談事や、内容に関して不明な点、ご質問、指摘事項、感想などございましたら、コメントやメールにてご連絡ください。
励みになるとともに、本ブログをよりたくさんの皆様に有益なものにできると考えています。
ぜひお待ちしております。
お問い合わせ先：surveyor_kenzo☆aol.com
※ご連絡の際は☆を@に変更してください。