必要な用語や手法に関する解説も一緒におこなっていきますので、参考書代わりに本記事を使ってみてください。
目次
令和4年測量士補試験No.12の問題文
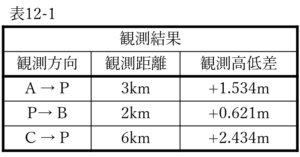
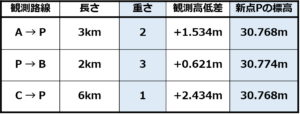
図 12 に示すように,既知点 A,B 及び C から新点 P の標高を求めるために公共測量における2 級水準測量を実施し,表 12-1 の結果を得た。新点 P の標高の最確値は幾らか。最も近いものを次の中から選べ。
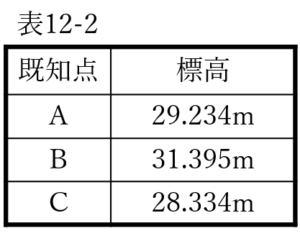
ただし,既知点の標高は表 12-2 のとおりとする。
なお,関数の値が必要な場合は,巻末の関数表を使用すること。
- 30.769 m
- 30.770 m
- 30.771 m
- 30.772 m
- 31.392 m
(令和4年測量士補試験問題集 No12)
令和4年測量士補試験No.12の解答・解説
「水準測量」の分野からの出題です。
解答は「3」となります。以下、詳しい計算手順の解説です。
計算に使用する関数表はコチラを参考にしてください。→関数表
新点Pの標高の最確値を求めるまでの考え方
標高の最確値を求める問題では、以下のようなステップで問題を解いていくのが基本です。
- 各観測路線の重さを考える
- 各観測点の観測成果から新点Pの標高を計算する
- 最確値の計算をおこなう
「観測路線の重さ」や「最確値」など水準測量ならではの言葉がだたびたび出てきます。
初学者の方には少しハードルが高い部分ではあるかもしれませんが、意味を知ればそれほど難しい言葉ではありません。
ただ、計算内容については覚える部分も多いので、次の章からそれぞれ詳しくかつわかりやすく説明を心がけていきます。
質問や分かりにくい場所があればコメントやメールなどで教えてください!
手順1 各観測路線の重さを考える
新点Pの標高の最確値を求める問題では、まず各観測路線の重さを考えることが重要になってきます。
このステップがキモと言っても過言ではないです。
まずは観測路線の重さのお話をしたいので、もう理解しています!という方は次の章へ読み進めていただいて大丈夫です。
逆に「観測路線の重さ」ってなに?な人や何となくまだ不安な人はまずは理解していきましょう!
観測路線の重さとは?
そもそも、各観測路線の重さとは何か…というお話ですがこれは
観測路線の成果をどれほど信じることができるかを表した数値
のことだと考えてもらえればいいです。
数字が大きいほど信頼度が高く、「0」に近づくほど信頼度が低くなります。
同じ地点の高さを複数路線から測ると観測路線の違いで観測距離などが変わってくるため、それぞれの路線からの同一地点に対する観測成果を比べたときに、どの路線をどのくらい信頼すべきかをランク付けする必要があるわけですね。
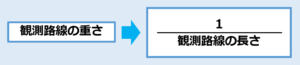
次に各観測路線の重さはどのように表すかというお話ですが、これは以下の関係で表します。
つまり「観測の重さは距離に反比例している」ということです。
例えば、観測路線の長さが
- 4mであれば1/4
- 8mであれば1/8
- 9mであれば1/9
のように表します。
観測路線が伸びれば伸びるほど分母の数が大きくなるので、結果的に数値がどんどん小さくなりますね。
さきほど「0」に近づくほど信頼度が低くなるというお話をしたので
観測距離が伸びる=観測成果の信頼度が低くなる
という関係が成り立つことが分かりますね。
本問の観測路線の重さの考え方
さて、話を戻しましてそれでは本問題では
- A→P
- P→B
- C→P
の3つの観測路線があります…それぞれの観測成果の重さはどのようになるのでしょうか?
観測路線の長さと重さの関係から、以下のように表すことができます。
さらに上表の重さを比で表してみます。分数のままだと各観測路線の重さの比率が分かりづらいので、整数に直しましょう。
 つまり、A→P:P→B:C→P=2:3:1の比率で観測路線の重さがあることが分かりました。
つまり、A→P:P→B:C→P=2:3:1の比率で観測路線の重さがあることが分かりました。
手順2 各観測点から新点Pの標高を計算する
手順1で観測路線の重さを導き出したら、次に各観測点の観測成果から新点Pの標高の計算をします。
標高の計算自体は
- 観測路線終了地点の標高=観測路線開始地点の標高+観測高低差
というシンプルなものです。
A→Bという観測路線があったときに観測高低差が+h mあったとしたら「AからBを見ると+h m高い場所になるんだな~」と考えてもらえたらいいと思います。
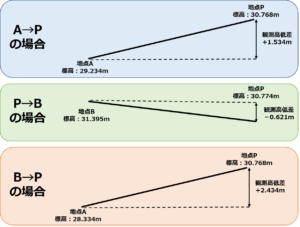
このことをそのまま図で表すとこのようになります。
さらに今回の問題に当てはめてみると、各観測路線での新点Pの標高はそれぞれ以下のように計算できますね。
A→Pの路線の新点Pの標高
=既知点Aの標高(29.234m)+観測高低差(+1.534m)
=30.768m
C→Pの路線の新点Pの標高
=既知点Cの標高(28.334m)+観測高低差(+2.434m)
=30.768m
P→Bも同様に…といきたいところですが、A→P・C→Pは観測終了地点がPになっているのに対して、P→Bは観測開始地点がPになっていますね。
つまり、P→Bの観測高低差である「+0.621m」はP地点から見たB地点が0.621m高い場所にあることを表すので、逆にB地点からP地点を見てみる(C→B)と0.621m低い場所にあるとも言えます。
0.621m低いということはC→Pのときの観測高低差は「-0.621m」になるということですね。
一言でまとめると「観測路線の方向が逆転すれば、観測高低差の符号も逆転する」ということです。
これをふまえてP→Bの路線をB→Pの路線と置き換えて新点Pの標高を計算すると
B→Pの路線の新点Pの標高
=既知点Bの標高(31.395m)+観測高低差(-0.621m)
=30.774m
となります。
それぞれの位置関係をまとめてみるとこうなりますね。
手順3 最確値の計算をおこなう
手順1で求めた観測路線の重さと新点Pの標高を元に、新点Pの標高の最確値の計算を行います。
まずは、今まで計算した内容を簡単に表にまとめてみましょう。
また、新点Pの標高の最確値を求める公式は以下のようになっています。
これを本問に置き換えると、次の様になります。
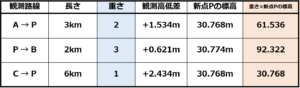
まずはわかりやすいように、各観測路線の重さ×新点Pの標高を出しちゃいましょう。
観測路線A→Pの重さ×新点Pの標高
=2×30.768m=61.536
観測路線P→Bの重さ×新点Pの標高
=3×30.774m=92.322
観測路線C→Pの重さ×新点Pの標高
=1×30.768m=30.768
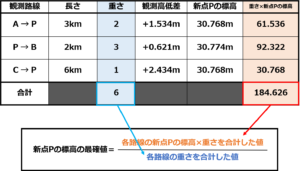
そしてこの各路線の重さ×新点Pの標高の値を先ほどまとめた表に追加します。
この表で青く着色した部分の合計値が最確値を求める公式の分母、赤く着色した部分の合計値が分子となります。
よって
新点Pの標高の最確値=184.626/6=30.771
となるので、正しい選択肢の値は「2」となります。
令和4年測量士補試験No.12のまとめ
「水準測量」からの出題でした。
今回は、新点の標高の最確値を求める問題でしたね。
公式の暗記や解き方のステップなど、覚えることはありますが出題頻度が高めなので習得必須の内容です!
ゆっくりと表を埋める感覚で解いていけばそこまで難しく感じないと思います!
得点源の1つになるように頑張りましょう!
令和4年測量士補試験No.12の類題
他年度の測量士補試験に出題された本問の類題です!ぜひチャレンジしてみてください!
令和3年測量士補試験問題集NO.13→問題文及び解説記事はコチラ
その他の測量士補試験の問題に挑戦!
令和4年のNO.12の問題を確認したら、その他の問題にも挑戦していきましょう!
本ブログでは各問題の解説を年度ごとに一覧にまとめたページがありますので、ぜひその記事からその他の問題に挑戦してみてください!
問題解説のまとめ記事はコチラからどうぞ!→過去問に挑戦!現役測量士の解説を読んで測量士補試験を攻略しよう!
さいごに
本ブログを参考にしていただきありがとうございます。
内容に関して不明な点、ご質問、指摘事項、感想などございましたら、コメントやメールにてご連絡ください。
励みになるとともに、本ブログをよりたくさんの皆様に有益なものにできると考えています。
ぜひお待ちしております。
お問い合わせ先:surveyor_kenzo☆aol.com
※ご連絡の際は☆を@に変更してください。

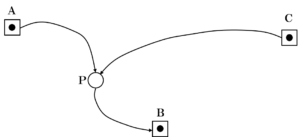 図12
図12