必要な用語や手法に関する解説も一緒におこなっていきますので、参考書代わりに本記事を使ってみてください。
目次
令和４年測量士補試験No.１１の問題文
次のａ～ｅの文は，水準測量の誤差について述べたものである。 （ア）～（オ）に入る語句の組合せとして最も適当なものはどれか。次の中から選べ。
- 標尺を 2 本 1 組とし，測点数を偶数とすることで，標尺の（ア）を軽減することができる。
- レベルと標尺の間隔が等距離となるように整置して観測することで，（イ）を軽減することができる。
- （ウ）は，地球表面が湾曲しているために生じる誤差である。
- 光の屈折による誤差を小さくするには，レベルと標尺の距離を（エ）して観測する。
- 公共測量におけるレベルによる水準測量において，往復観測値の較差の許容範囲は，観測距離の（オ）に比例する。
- （ア）零点誤差（イ）視準線誤差（ウ）球差（エ）長く（オ）二乗
- （ア）目盛誤差（イ）視準線誤差（ウ）気差（エ）短く（オ）平方根
- （ア）零点誤差（イ）鉛直軸誤差（ウ）球差（エ）長く（オ）二乗
- （ア）零点誤差（イ）視準線誤差（ウ）球差（エ）短く（オ）平方根
- （ア）目盛誤差（イ）鉛直軸誤差（ウ）気差（エ）長く（オ）二乗
（令和4年測量士補試験問題集 No１１）
令和４年測量士補試験No.１１の解答・解説
「水準測量」の分野からの出題です。
解答は「２」となります。以下、各項目の詳しい解説です。
（ア）について
『標尺を 2 本 1 組とし，測点数を偶数とすることで，標尺の（ア）を軽減することができる。』
（ア）には「零点誤差」と「目盛誤差」のうち「零点誤差」が入ります。
「零点誤差」と「目盛誤差」それぞれの解説について詳しく見ていきましょう！
零点誤差とは
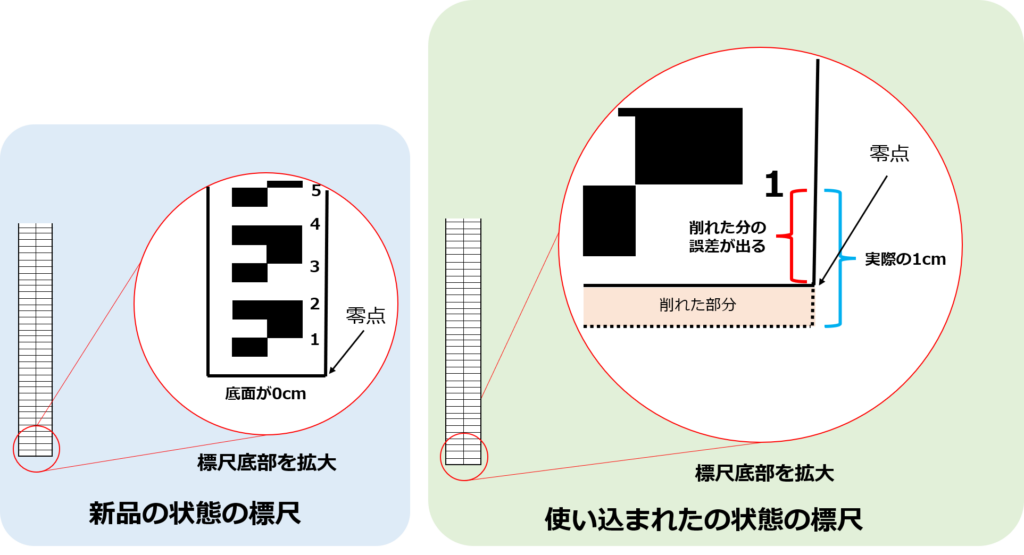
零点誤差とは、標尺の下端部分が擦り減っていくことで発生する誤差のことです。
標尺の下端部分のことを零点と言い、日々の水準測量の作業の中で標尺を使い続けることでどんどん零の位置が擦り減り、変わってしまいます。
この零点誤差の対応として有効なのが、標尺を2本1組で使用することを前提とした
- 標尺の設置回数を奇数回にする
- レベルを据える回数（測点数）を偶数にする
といった対応です。
これらは言葉を言い換えているだけで、両方とも同じ行動をとります。
レベルを据える回数（測点数）を偶数回にする（標尺の設置回数を奇数回にする）ことで、出発点と終着点に同じ標尺を使用できますね。
これが結果的に出発点の後視と終着点の前視で同じ標尺を観測することとなり、零点誤差を相殺することができます。
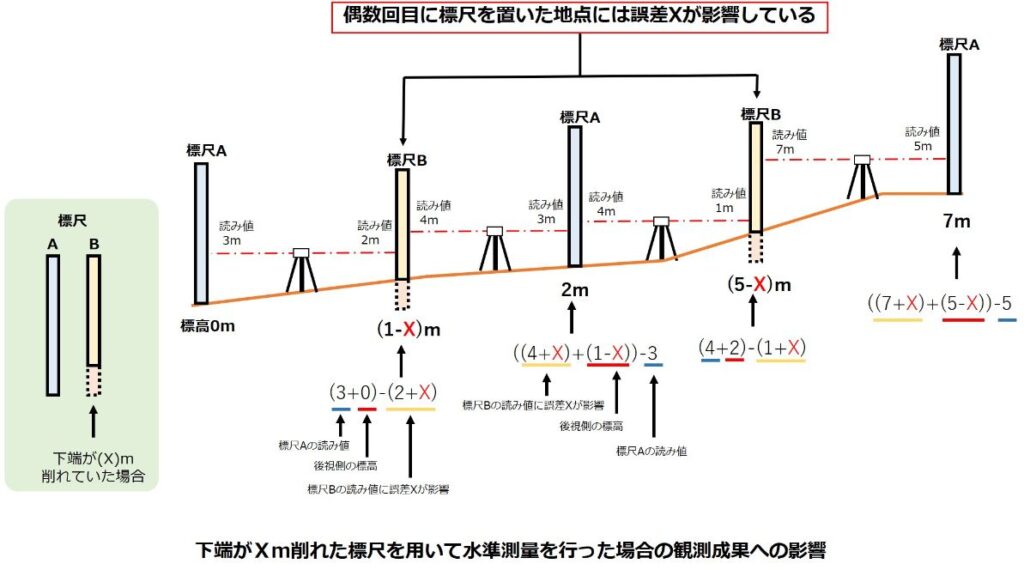
言葉にしても原理が良くわからないと思うので、実際に図で表して計算してみるとよくわかります。
図の左側から右側へ向かって観測を進めていくと仮定して各観測点ごとの標高を計算していくと、偶数回目に標尺を据える地点にだけXmの誤差が残っていることが分かりますね。
逆に奇数回目には誤差が残っていません。
このことからも
- 標尺の設置回数を奇数回にする
- レベルを据える回数（測点数）を偶数にする
といった対応が有効であることが分かります。
目盛誤差とは
目盛誤差は、名前の通り標尺の持つ目盛と実際の高さの差のことです。
標尺に刻まれている目盛が正しくないことが原因で起こる誤差となります。
標尺そのものが持っている誤差で、1つ1つの標尺の個性と言っても良いでしょう。
ただ、基本的に測量で使用する標尺は第三者機関による測量機器の検定を通っていることを前提としているので、あくまでその誤差は小さなものです。
そんな目盛誤差に対応するためには、
- 往復で観測する際に、往路の終着点と復路の出発点の標尺を入れ替えること
が有効な手段となります。
往路と復路それぞれで通る同じポイントに同一の標尺が立たないようにすることで誤差の影響にかたよりがなくなり、目盛誤差を小さくすることができます。
「零点誤差」と「目盛誤差」それぞれの説明内容から、（ア）に入る言葉は「零点誤差」が適切であると考えられます。
（イ）について
『レベルと標尺の間隔が等距離となるように整置して観測することで，（イ）を軽減することができる。』
（イ）には「視準線誤差」と「鉛直軸誤差」のうち「視準線誤差」が入ります。
「視準線誤差」と「鉛直軸誤差」それぞれの解説について詳しく見ていきましょう！
視準軸誤差とは
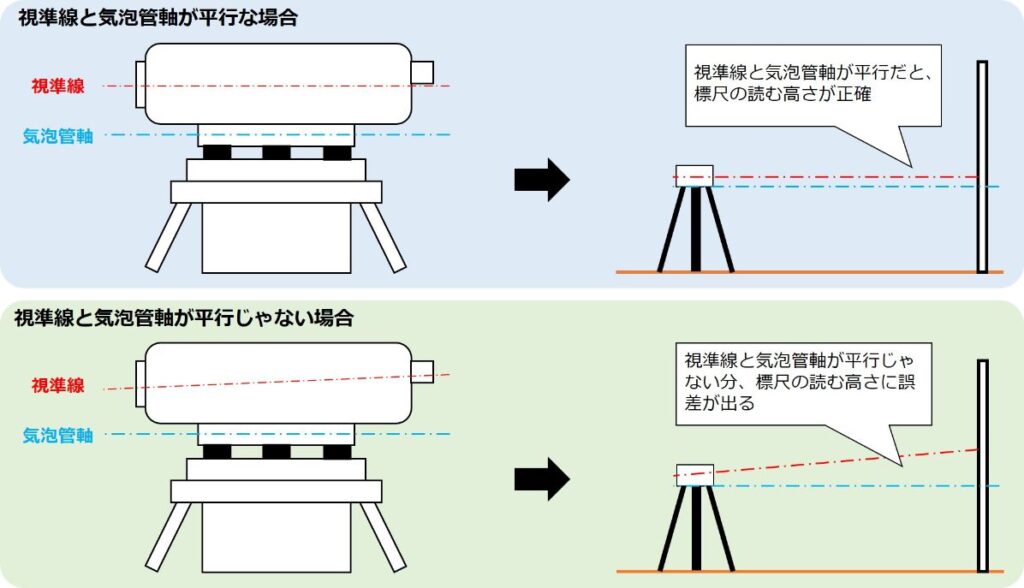
視準線誤差は
- 気泡管軸
- 視準線
の2つが平行ではないために起こってしまう誤差です。
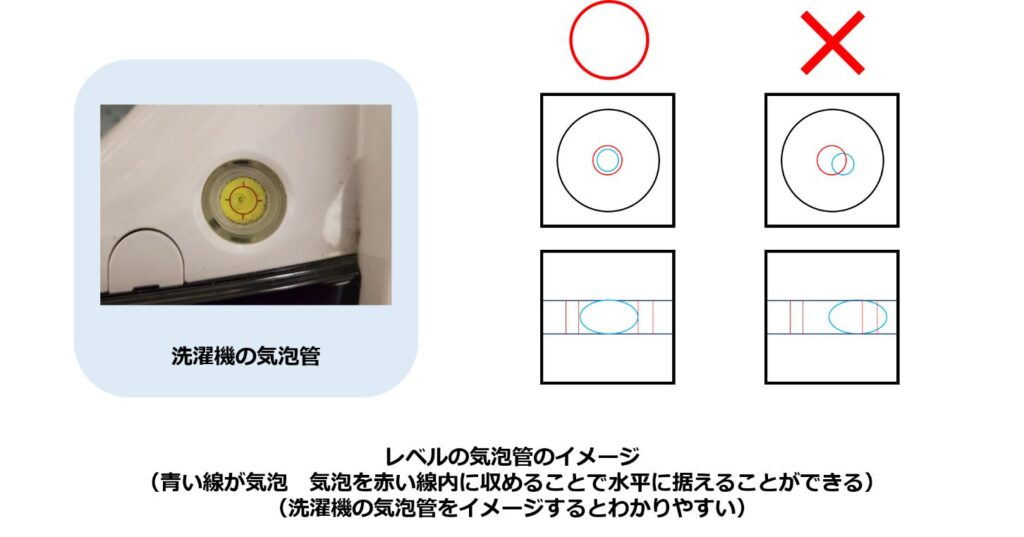
レベルを設置する際には、器械についている気泡管を参考に「器械が水平かどうか」を確認します。
（レベルを見たことがない方は、家にある洗濯機などについている気泡管をイメージしてください。）
ただ、気泡管を使って器械を水平に保っても実際に視準するレンズ部分がその気泡管と平行になっていなければ、その状態で高さを観測しても正しい値とはいえません。
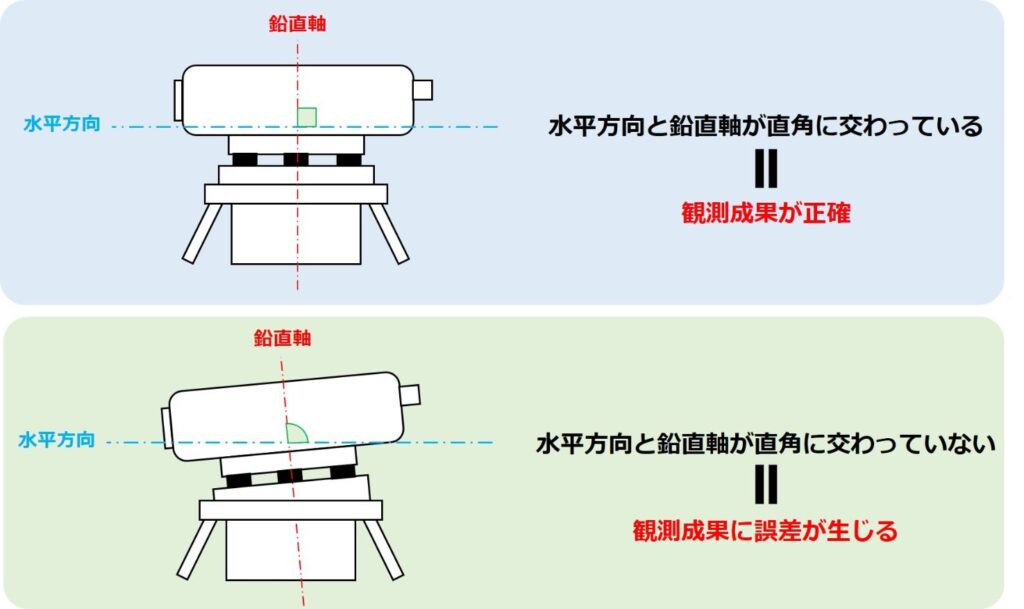
例えば上の図では視準線と気泡管軸が平行になっているのでレベルから標尺までの視準線が水平になっていますが、下の図では視準線と気泡管軸が平行になっていないため視準線が水平にならず、標尺の目盛を読んだときに誤差が生じてしまっています。
それでは、この視準線誤差はどのように小さくすればいいのでしょうか。
方法は次の2つです。
- センターレベリング
- 杭打ち調整法
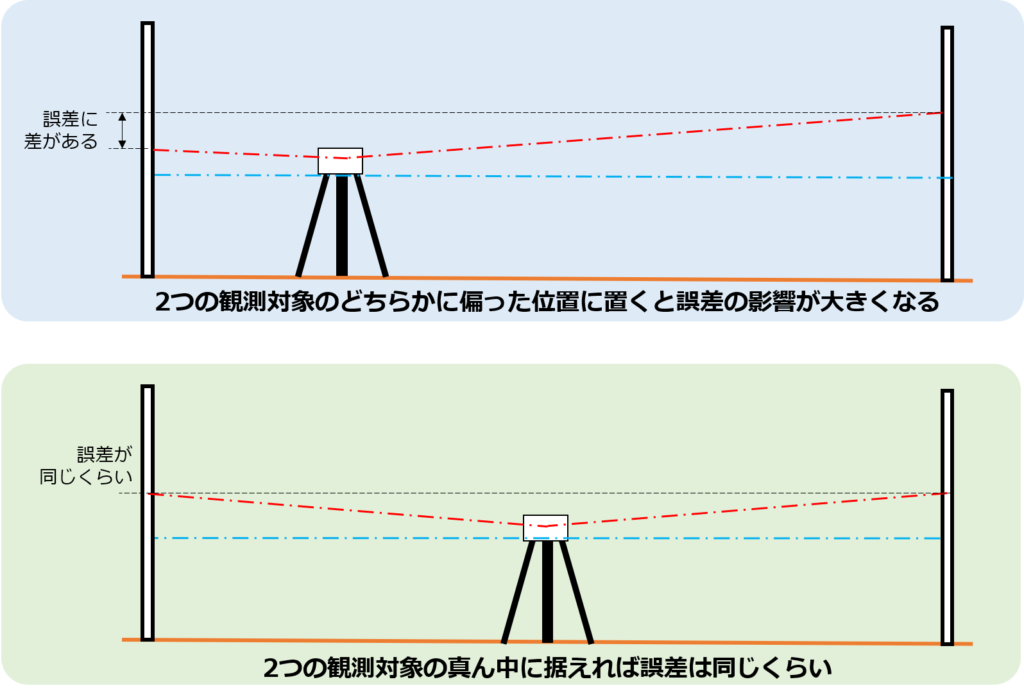
センターレベリングは名前にセンター（中央）が入っているように、2つの標尺から等距離にあたる真ん中の位置にレベルをおいて観測する手法です。
中央に置くことで、視準線誤差による観測結果への影響を少なくすることができます。
また、レベルを設置する場所は2つの標尺を結んだ直線状にすることも重要になってきます。
上の図ではレベルを片方の標尺側にかたよって設置しているので、それぞれの標尺の読み値が持つ誤差に差が出てしまっています。
一方で下の図ではセンターレベリングにより2つの標尺のちょうど真ん中あたりにレベルを設置しているので、誤差の差が小さいです。
上記のようにセンターレベリングでは観測する方法で誤差を小さくしていますが、一方で杭打ち調整法では器械の視準線そのものを調整して誤差を小さくします。
今回の問題に関してはそこまでの知識は不要ですので、杭打ち調整法の詳しい解説についてはまた別の記事で紹介します。
視準軸誤差に関してまとめると以下のようになります。
| 誤差名 | 原因 | 対処法 |
| 視準軸誤差 | 気泡管軸と視準線が平行でない | ・センターレベリング ・杭打ち調整法 |
鉛直軸誤差とは
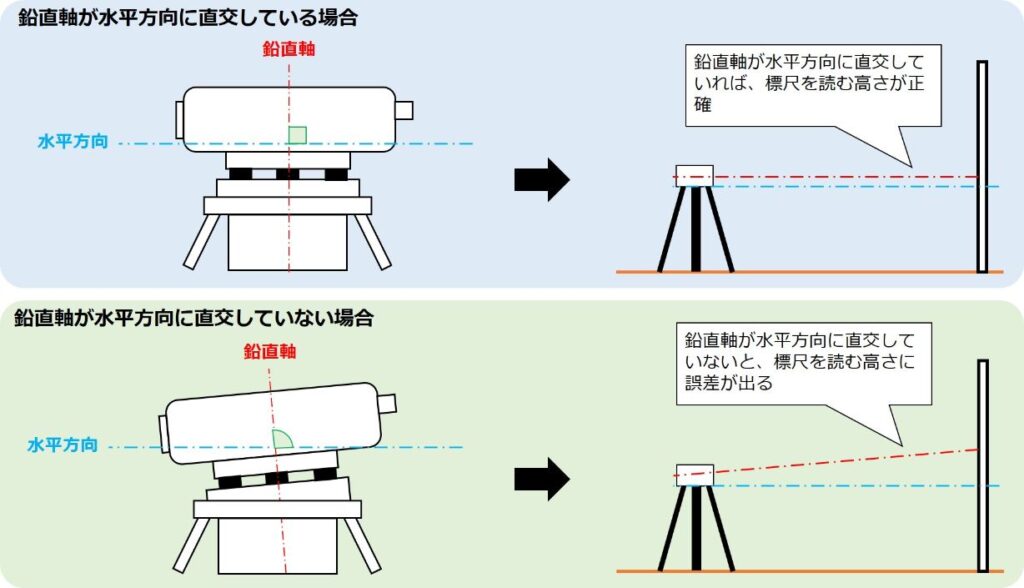
鉛直軸誤差は、レベルの鉛直軸が水平方向と鉛直ではないために起こる誤差です。
鉛直軸誤差も視準線誤差と同様に、標尺で読む高さに誤差が生じてしまいます。
視準線誤差の場合はセンターレベリングで対応できましたが、鉛直軸誤差の場合はそうはいきません。
視準線誤差はあくまで視準線の傾きの誤差のため前視と後視の観測の切り替え時に誤差の影響が出ていました。
一方で鉛直軸誤差は器械そのものの軸が傾いてしまっているため、三脚を据えた段階で誤差による影響が出てしまうのです。
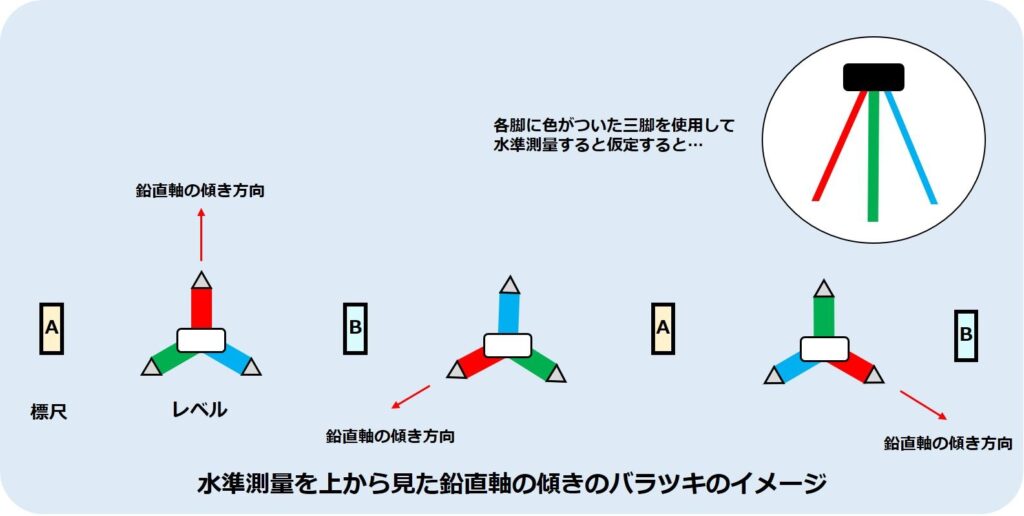
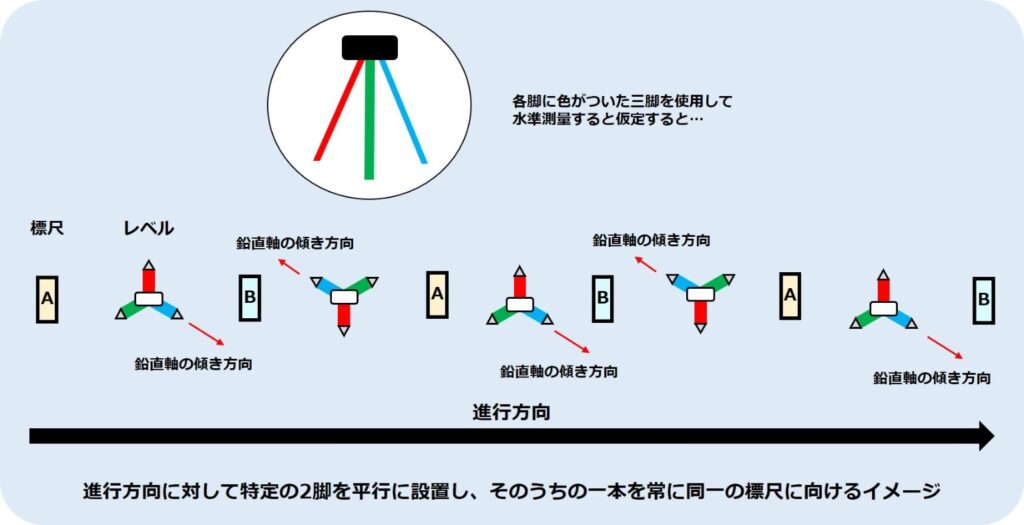
例えば上図のよう赤色の脚側に鉛直軸が傾いてしまっているとします。その結果、据えるたびに傾いている軸の方向が変わってしまい、誤差の値がばらつくので対応することができません。
それでは、どのように対応するのが正解なのでしょうか…答えは次の通りです。
- レベルと三脚の特定の２脚を進行方向に平行に整置し，そのうちの１本を常に同一の標尺に向けて観測する
これを図で表すと次の様になります。
進行方向に対して特定の2脚を平行に設置（上図では青と緑の脚）し、そのうちの一本を同一の標尺に向けています（上図では緑の脚を標尺Aに、青の脚を標尺Bに向けている）。
こうすることで常に軸の傾く方向を片方の標尺側に保つことができ、レベルで読み取る高さの誤差への影響を少なくすることができるのです。
また、レベルの整準をする際に望遠鏡を特定の標尺に向けて行うことも有効な対応です。
よって今までのことをまとめますと、次の表のようになります。
| 誤差名 | 原因 | 対処法 |
| 鉛直軸誤差 | 鉛直軸が水平方向と垂直に交わっていない | ・進行方向に対し特定の2脚を平行に設置、およびそのうちの一本を同一の標尺へ向ける ・整準をする際に望遠鏡を特定の標尺に向けて行う |
「視準線誤差」と「鉛直軸誤差」のそれぞれの説明から（イ）には「視準線誤差」が適切であると考えられます。
（ウ）について
『（ウ）は，地球表面が湾曲しているために生じる誤差である。』
（ウ）には「球差」と「気差」のうち「球差」が入ります。
「球差」と「気差」それぞれの解説について詳しく見ていきましょう！
球差とは
地球が丸い（＝湾曲している）ことが影響して、本来読むべき数値とレベルで視準した数値に差が出てしまうことを言います。
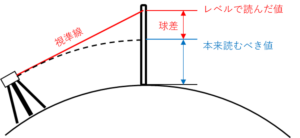レベルで視準している方向は地球の丸さの影響を受けないため、上の図のような差（＝球差）が発生します。
気差とは
空気の影響で光が屈折することで、本来読むべき数値とレベルで視準した数値に差が出てしまうことを言います。
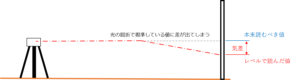レベルで視準している線が標尺までの間で屈折してしまい、上の図のような差（気差）が発生します。
本問の（ウ）では、地球表面が湾曲しているために生じている誤差に関して書いているので、（ウ）には「球差」が適切であると考えられます。
（エ）について
『光の屈折による誤差を小さくするには，レベルと標尺の距離を（エ）して観測する。』
（エ）には「長く」と「短く」のうち「短く」が入ります。
なぜ光の屈折による誤差は、レベルと標尺の距離を短くして観測すると小さくなるのでしょうか？
光の屈折による誤差は、レベルから標尺までの間に空気の層があることで発生します。
レベルから標尺までの距離が長くなるほど空気の層が増えますので、その分観測する値への影響も大きくなります。
よって（エ）には「短く」という言葉が適切であると考えられます。
（オ）について
『公共測量におけるレベルによる水準測量において，往復観測値の較差の許容範囲は，観測距離の（オ）に比例する。』
（オ）には「二乗」と「平方根」のうち「平方根」が入ります。
国土地理院が定める作業規程の準則の第３章 第５節 第６５条に往復観測値の較差の許容範囲について以下のように記載があります。
- 1級水準測量：2.5mm√S
- 1級水準測量：5mm√S
- 1級水準測量：10mm√S
- 1級水準測量：20mm√S
※Ｓは観測距離
（作業規程の準則 P35）
上記内容から、観測距離の平方根（√）が往復観測値の較差の許容範囲に比例していることが分かります。
よって（オ）には「平方根」が適切であると考えられます。
令和４年測量士補試験No.１１のまとめ
「水準測量」からの出題でした。
水準測量の誤差の原因や対策・対応は毎年のように出題があるとても重要な問題です。
類題も含み様々なパターンの過去の問題を解いて、必ず対応出来るようにしましょう！
その他の測量士補試験の問題に挑戦！
令和4年のNO.11の問題を確認したら、その他の問題にも挑戦していきましょう！
本ブログでは各問題の解説を年度ごとに一覧にまとめたページがありますので、ぜひその記事からその他の問題に挑戦してみてください！
問題解説のまとめ記事はコチラからどうぞ！→過去問に挑戦！現役測量士の解説を読んで測量士補試験を攻略しよう！
令和４年測量士補試験No.１１の類題
過去に出題された本問の類題です！ぜひチャレンジしてみてください！
令和2年測量士補試験問題集NO.10→問題文及び解説記事はコチラ
令和3年測量士補試験問題集NO.10→問題文及び解説記事はコチラ
令和3年測量士補試験問題集NO.11→問題文及び解説記事はコチラ
令和4年測量士補試験問題集NO.10→問題文及び解説記事はコチラ
さいごに
本ブログを参考にしていただきありがとうございます。
内容に関して不明な点、ご質問、指摘事項、感想などございましたら、コメントやメールにてご連絡ください。
励みになるとともに、本ブログをよりたくさんの皆様に有益なものにできると考えています。
ぜひお待ちしております。
お問い合わせ先：surveyor_kenzo☆aol.com
※ご連絡の際は☆を@に変更してください。