必要な用語や手法に関する解説も一緒におこなっていきますので、参考書代わりに本記事を使ってみてください。
目次
令和3年測量士補試験No.3の問題文
次の文の(ア)及び(イ)に入る数値の組合せとして最も適当なものはどれか。次の中から選べ。
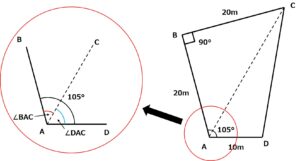
なお,関数の値が必要な場合は,巻末の関数表を使用すること。点 A,B,C,D で囲まれた四角形の平たんな土地 ABCD について,幾つかの辺長と角度を観測したところ,∠ABC=90 °,∠DAB = 105 °,AB = BC = 20 m,AD = 10 m であった。
このとき AC =(ア)mであり,土地 ABCD の面積は(イ)㎡ である。(回答群)
1.(ア)28.284(イ)270.711
2.(ア)28.284(イ)322.475
3.(ア)34.641(イ)150.000
4.(ア)34.641(イ)286.603
5.(ア)34.641(イ)340.000(令和3年測量士補試験問題集 No.3より)
令和3年測量士補試験No.3の解答・解説
「測量に関する法規」の分野からの出題になります。
解答は「2」となります。以下、詳しい計算手順の解説です。
1.問題文にある数値から図形を書いてみる
問題文を読んでいくと、以下の情報がわかります。
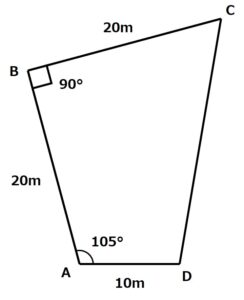
- 四角形の平たんな土地ABCD
- ∠ABC=90 °
- ∠DAB = 105 °
- AB = BC = 20 m
- AD = 10 m
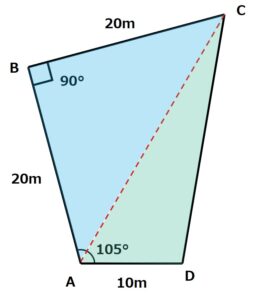
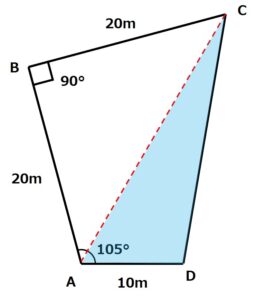
この情報をもとに図形を書いてみると、次のようになります。
2.補助線ACを引いて2つの三角形を作成する
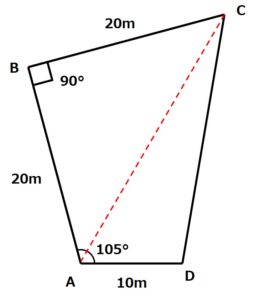
問題文で辺ACの長さを問われているため、まずは辺ACを作成します。
AからCに向かって補助線ACを引くと、四角形ABCDの中を三角形ABCと三角形ACDにわけることができます。
3.辺ACの長さを求める。
まずは、問題文でも聞かれている辺ACの長さを考えてみましょう。
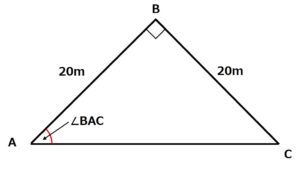
ここで、辺ACを持つ三角形ABCについて見てみます。
三角形ABCをよく見てみると、
- ∠ABC=90°(直角)
- AB=AC=20m
の条件を持った直角二等辺三角形であることがわかりますね!
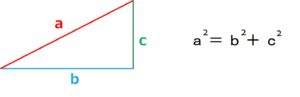
直角三角形の辺の長さを考えるときは、中学の数学で習う三平方の定理が使えないか考えてみます。
三平方の定理とはこんなやつですね。
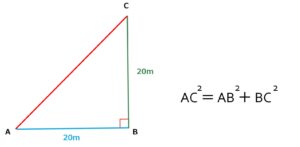
これを三角形ABCに当てはめてみると以下のような感じになります。
よって、この式を計算してACを求めてみると
AC^2=AB^2+BC^2
AC=√(20)^2+(20)^2
=√(400+400)
=√800
=20√2
=20×1.41421356…
≒28.28426…
≒28.284…
となります。
よってAC=28.284mです。
4.四角形ABCDの面積の出し方を考える
四角形ABCDの面積を出すにはどのようにすればよいのでしょうか?
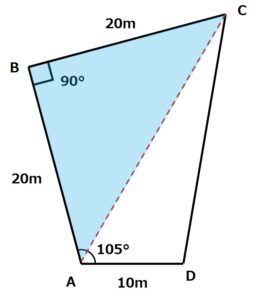
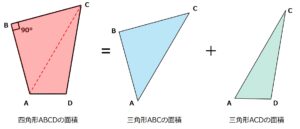
補助線ACを引いたことで、現在四角形の中は三角形ABCと三角形ACDに分けることができています。
つまり四角形ABCDの面積を出すには、三角形ABCとACDの面積を出せば良さそうです。
というわけで、次の手順から三角形ABCと三角形ACDの面積の出し方を考えてみます!
5.三角形ABCの面積を出す
まずは三角形ABCの面積を出します。
手順3で三角形ABCは
- ∠ABC=90°(直角)
- AB=AC=20m
の条件を持った直角二等辺三角形であることがわかりました。
直角二等辺三角形の面積は小学校で習った三角形の面積を求める公式「底辺×高さ÷2」で求めれば一発で出ますので、
今回の三角形ABCにも、その公式を当てはめてみます。
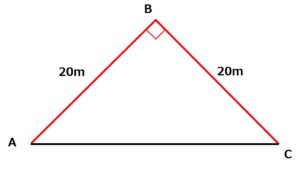
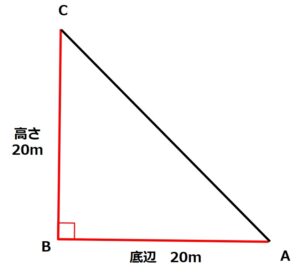
底辺と高さが分かりやすいように三角形ABCくるっと回転させてみると次の画像のようになるので…
三角形ABCの面積
=底辺×高さ÷2
=20m×20m÷2
=200㎡
となります。
よって三角形ABCの面積は「200㎡」です。
6.三角形ACDの面積を出す
続いて三角形ACDの面積を出します。
三角形ACDのように直角がない三角形の場合は、三角関数で習うsin(サイン)を使用した面積の計算を考えてみます。
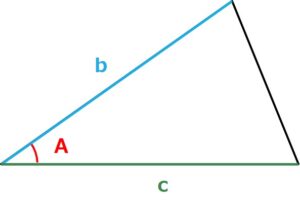
sinを用いた面積の公式は
三角形の面積=(1/2)×b×c×sinA
と高校数学で習っています。
今回は、
- ∠DAB=105°
- AD=10m
という条件が与えられているので、そちらに着目してみましょう!
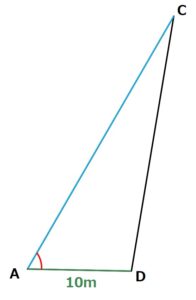
三角形ACDを公式に当てはまるように考えてみると
- ∠DAC
- AC
- AD
が使えそうです!
ACは手順3で求めて28.284mであることがわかっていますし…
∠DABから∠BACを引けば、∠DACが求められそうです…
というわけで…まずは∠DACを求めるために∠BACを求めます。
∠BACを求める
∠DACを求めるためには∠DABから∠BACを引く必要がありそうですが、∠BACの角度はまだわかっていません。
そのため、まずは∠BACを求めてみます。
∠BACは1つ前の手順で面積を求めた三角形ABCが持つ角度です。
直角二等辺三角形の角度は「直角以外のそれぞれの角度が45°と決まっている」ので、∠BACは45°となります。
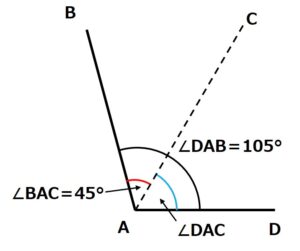
∠DACを求める
前述しましたが、∠DACは∠DABから∠BACを引くことで求めることができます。
式で表すと
∠DAC=∠DAB-∠BAC
です。
問題文で∠DAB=105°、計算で∠BAC=45°と分かっているので、
∠DAC
=∠DAB-∠BAC
=105°-45°
=60°
と計算できます。
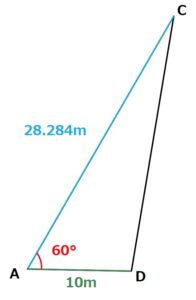
三角形ACDの面積を求める
これまでの手順で三角形ACDを求めるために必要な
- ∠DAC
- AC
- AD
の数値が出そろいました!
ここで改めて三角形ACDの面積を求めるための公式を考えてみます。
sinを用いた面積の公式は
三角形の面積=(1/2)×b×c×sinA
ですので、今回の三角形ACDに当てはめると
三角形ACDの面積=(1/2)×AC×AD×sin(∠DAC)
となります。
よってこれを計算していくと
三角形ACDの面積=(1/2)×28.284×10×sin(60°)
関数表からsin60°=0.86603なので
=(1/2)×28.284×10×0.86603
≒122.4740
よって、三角形ACDの面積≒122.4740㎡となります。
7.四角形ABCDの面積を出す
長い道のりでしたが、あとは三角形ABCと三角形ACDの面積をたして、四角形ABCDの面積を出すだけです。
手順5で三角形ABCの面積=200㎡
手順6で三角形ACDの面積=122.4740㎡
であることがわかりました。
よって
四角形ABCDの面積=三角形ACDの面積+三角形ACDの面積
=200㎡+122.4740㎡
=322.4740㎡
となりますので、四角形ABCDの面積=322.4740㎡です。
回答群には322.475と書いてありますが、計算に利用する小数点以下の数値をどこまで使用するかで多少変わってきます。
そのため気にしなくて大丈夫です。
AC=28.284、四角形ABCD=322.474なので、最も近い値の組み合わせを持つ(イ)が答えになります。
令和3年測量士補試験No.3のまとめ
今回は面積計算に関する出題でした。
計算過程を詳しく説明しているので、解答までの道のりを長く感じたかもしれませんが何度か解いてパターンを覚えれば大丈夫です!
過去に学校で習ったことを思い出しながらマスターしていきましょう!
その他の測量士補試験の問題に挑戦!
令和3年のNO.3の問題を確認したら、その他の問題にも挑戦していきましょう!
本ブログでは各問題の解説を年度ごとに一覧にまとめたページがありますので、ぜひその記事からその他の問題に挑戦してみてください!
問題解説のまとめ記事はコチラからどうぞ!→過去問に挑戦!現役測量士の解説を読んで測量士補試験を攻略しよう!
さいごに
本ブログを参考にしていただきありがとうございます。
内容に関して不明な点、ご質問、指摘事項、感想などございましたら、コメントやメールにてご連絡ください。
励みになるとともに、本ブログをよりたくさんの皆様に有益なものにできると考えています。
ぜひお待ちしております。
お問い合わせ先:surveyor_kenzo☆aol.com
※ご連絡の際は☆を@に変更してください。