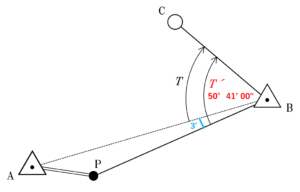st-kaiwa1]この記事を書いているのは現役の測量士です。本記事では令和４年測量士補試験のNo.７の内容について詳しく解説していきます。
必要な用語や手法に関する解説も一緒におこなっていきますので、参考書代わりに本記事を使ってみてください。[/st-kaiwa1]
目次
令和４年測量士補試験No.７の問題文
図7は，トータルステーションによる偏心観測について示したものである。図 7 のように，既知点 B において，既知点 A を基準方向として新点 C 方向の水平角を測定しようとしたところ，既知点 B から既知点 A への視通が確保できなかったため，既知点 A に偏心点 P を設けて，水平角 T ′，偏心距離 e 及び偏心角 Φ の観測を行い，表 7 の結果を得た。このとき，既知点 A 方向と新点 C 方向の間の水平角 T は幾らか。最も近いものを次の中から選べ。
ただし，既知点 A，B 間の距離 S は，1,500m であり，S 及び e は基準面上の距離に補正されているものとする。
また，角度 1 ラジアンは，（2×10^(5乗)）″ とする。
なお，関数の値が必要な場合は，巻末の関数表を使用すること。表７
Φ 210° 00’ 00" e 2.70 m T´ 50° 41’ 00"
- 50°30’ 00"
- 50°32’ 00"
- 50°34’ 00"
- 50°36’ 00"
- 50°38’ 00"
（令和4年測量士補試験問題集 No７）
令和４年測量士補試験No.７の解答・解説
「多角測量」の分野からの出題です。
解答は「５」となります。
以下、本問についての詳しい計算手順です。
計算に使用する関数表はコチラを参考にしてください。→関数表
水平角Ｔを求めるための計算手順
水平角Tを求めるためには、以下の手順を踏んでいきます。
- 問題文からわかる情報を図に書き込む
- Ｔ´とＴの角度の差を求める
- Ｔを求める
それでは、それぞれの手順について詳しく解説していきます！
手順１ 問題文からわかる情報を図に書き込む
まずは、問題文からわかる情報を整理していきます。
問題文及び表７から、以下の数値が読み取れます。
- AB間の距離S＝1,500m
- 偏心角Φ＝210° 00’ 00"
- 偏心距離e＝2.70m
- 水平角T´＝50° 41’ 00"
上記のそれぞれの数値を図７に書き込むと以下の通りです。
上の図をよく見てみると、既知点A、Bと偏心点Pが作る三角形に、問題文からわかる数値全てが関わっていることが分かります。
そこで、次の手順では三角形ABPを利用してT´（50° 41′ 00″）とTの角度の差を求めていきます。
手順２ T´とTの角度の差を求める
本問ではTを求めることが目的です。
三角形ABPのうちの∠ABPがわかればT´から∠ABPをひくことでTの角度を求めることができそうですね。
そこで∠ABP＝Xとして手順１で書いた図に追加します。
ここで、改めて三角形ABPについて注目してみましょう。
三角形ABPの∠Pについては、三角形の外側の角度が210°とわかっています。
そのため内側の角度は「360°－210°＝150°」となります。
以上のことをふまえて三角形ABPを図に表すと次のようになります。
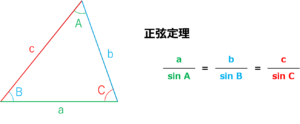
この三角形ABPでわかっている数値の位置関係から、今回は正弦定理という定理を使用します。
正弦定理とは、下図のように三角形の各辺・各角度のsinの値が持つ関係性のことです。
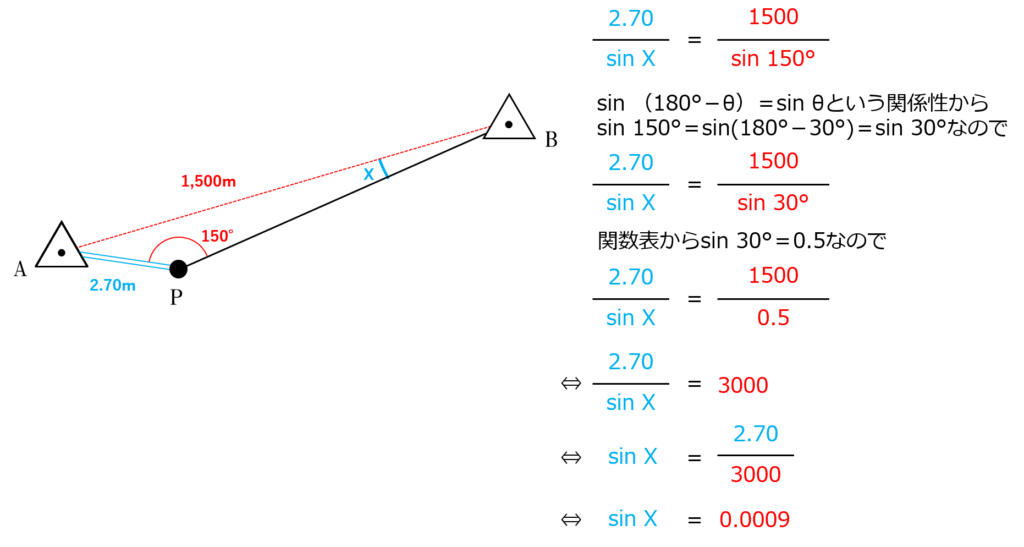
本問の三角形ABPに当てはめてみると、着色した部分が正弦定理のセットになります。
よって正弦定理から
となり、sin X＝0.0009となります。
sinの値が小さいとき（＝大体0.1まで）は「sinの値が角度（ラジアン）になる」の関係が成り立つので
sin X＝0.0009より
X＝0.0009（ラジアン）
となります。
問題文から、1ラジアンは2×10^(5乗)″とすることがわかっているので、
X＝0.0009（ラジアン）
＝0.0009×2×10^(5乗)″
＝180″
60″＝1′より
180″＝3′
よってX=180″＝3′
となり、角度Xが3′であることがわかりました。
手順３ Ｔを求める
手順２では、Ｔを求めるために必要なXを求めました。
X＝3′だったので、該当する箇所を図にまとめると以下のようになります。
Ｔ´から3′を差し引けばＴの値が出そうですね。
よって
Ｔ＝Ｔ´－3′
＝50° 41′ 00″－3′
＝50°38′00″
となり、Ｔ＝50°38′00″となりました。
選択肢と比べると５の数値が一致しますので、本問の解答は「５」となります。
令和４年測量士補試験No.７のまとめ
「多角測量」からの出題でした。
偏心による角度の問題は、非常によく出る問題です。
毎回路線の形状は違えど、やることは変わらないのでしっかりと解答方法を覚えて、得点源の1つにしていきましょう！
その他の測量士補試験の問題に挑戦！
令和4年のNO.7の問題を確認したら、その他の問題にも挑戦していきましょう！
本ブログでは各問題の解説を年度ごとに一覧にまとめたページがありますので、ぜひその記事からその他の問題に挑戦してみてください！
問題解説のまとめ記事はコチラからどうぞ！→過去問に挑戦！現役測量士の解説を読んで測量士補試験を攻略しよう！
さいごに
本ブログを参考にしていただきありがとうございます。
内容に関して不明な点、ご質問、指摘事項、感想などございましたら、コメントやメールにてご連絡ください。
励みになるとともに、本ブログをよりたくさんの皆様に有益なものにできると考えています。
ぜひお待ちしております。
お問い合わせ先：surveyor_kenzo☆aol.com
※ご連絡の際は☆を@に変更してください。