必要な用語や手法に関する解説も一緒におこなっていきますので、参考書代わりに本記事を使ってみてください。
目次
令和３年測量士補試験No.１９の問題文
画面距離 10 cm，撮像面での素子寸法 10 μm のデジタル航空カメラを用いて，対地高度2,000 m から平たんな土地について，鉛直下に向けて空中写真を撮影した。空中写真には，東西方向に並んだ同じ高さの二つの高塔 A，B が写っている。地理院地図上で計測した高塔 A，B 間の距離が 800 m，空中写真上で高塔 A，B の先端どうしの間にある画素数を 4,200 画素とすると，この高塔の高さは幾らか。最も近いものを次の中から選べ。
ただし，撮影コースは南北方向とする。
また，高塔 A，B は鉛直方向にまっすぐに立ち，それらの先端の太さは考慮に入れないものとする。
なお，関数の値が必要な場合は，巻末の関数表を使用すること。
- 40m
- 53m
- 64m
- 84m
- 95m
（令和3年測量士補試験問題集 No19より）
令和３年測量士補試験No.１９の解答・解説
「写真測量」の分野からの出題です。
解答は「５」となります。以下、詳しい計算手順の解説です。
計算に使用する関数表はコチラを参考にしてください。→関数表
高塔の高さを導くまでの考え方
本問は、高塔の高さの値を求める問題です。
高塔の高さの値を導くためには以下の手順を踏む必要があります。
- 問題文からわかる情報を図に書き出す
- 高塔の先端からの撮影高度を求める
- 高塔の高さを求める
また、事前知識として問題文にあるそれぞれの用語を整理しましょう。
既に知識がある！という方は次の章に進んでいただいても大丈夫です。
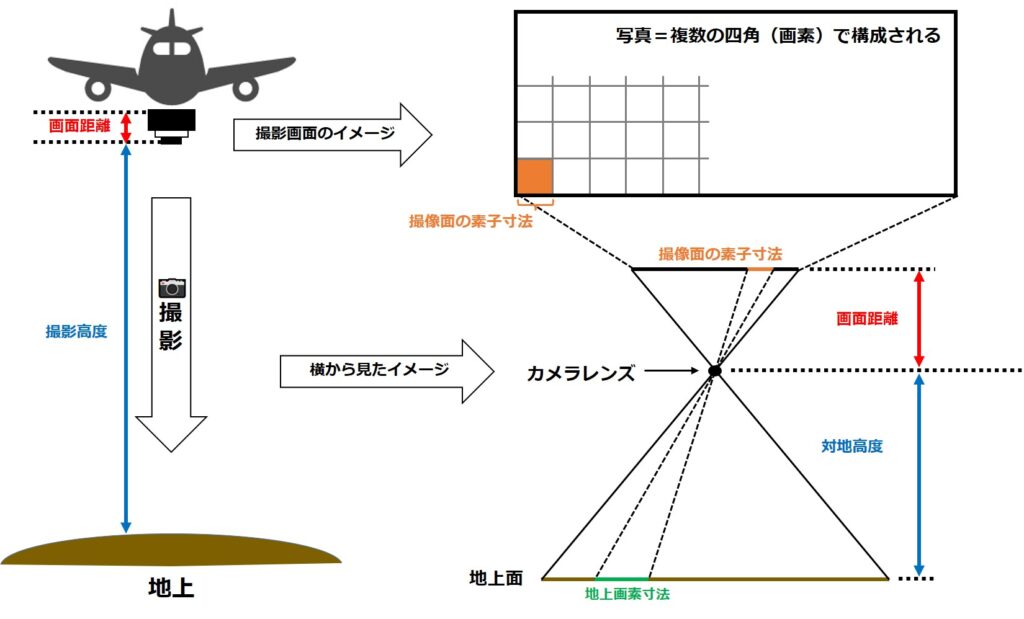
- 画面距離→レンズから撮像面までの距離
- 撮像面の素子寸法→1画素当たりの大きさ
- 対地高度→地面からレンズまでの高さ
- 地上画素寸法→撮影した際の1画素当たりに収まる実際の地面の大きさ
というイメージを持っていただければ大丈夫です。
それでは以上の内容を念頭に置いて実際に計算していきましょう！
手順１ 問題文からわかる情報を図に書き出す
まずは問題文に書いてある情報を整理するために、それぞれの数値や条件を図に書き出してみます。
問題文からは
- 画面距離 10cm
- 撮像面での素子寸法 10 μm
- 対地高度 2,000m
- 高塔A，Bは東西に並び高さが同じ
- 高塔A，Bの距離は800m
- 高塔A，Bの先端同士の間の画素数は4,200
ということがわかっています。
この段階で「画面距離」と「撮像面での素子寸法」の単位がmになっていないので計算しやすいようにmに変換しておきます。
cm→mにする際は「×0.01」、μm→mにする際は「×0.000001」をすることで単位を変換できますので、それぞれ
- 画面距離 10cm→10×0.01→0.1m
- 撮像面での素子寸法 10 μm→10×0.000001→0.00001m
となります。
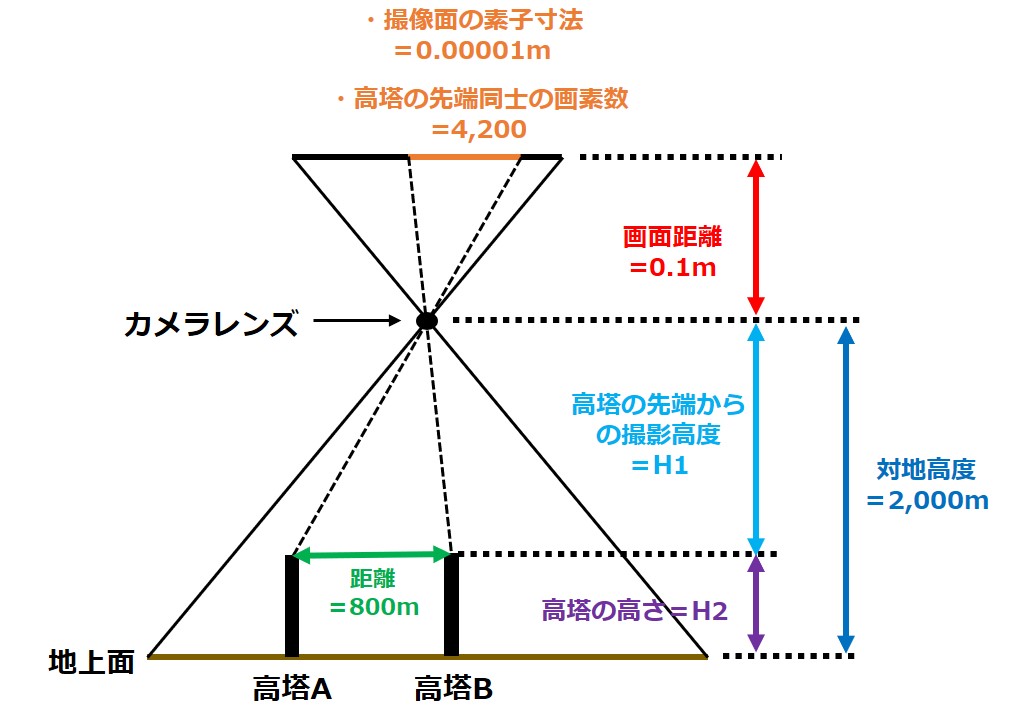
これらの数値を図に書き出すと以下のようになります。
手順２からはこの図をもとに解いていきましょう！
手順２ 高塔の先端からの撮影高度を求める
高塔の先端からの撮影高度を求めるためには、三角形の相似の計算を利用していきます。
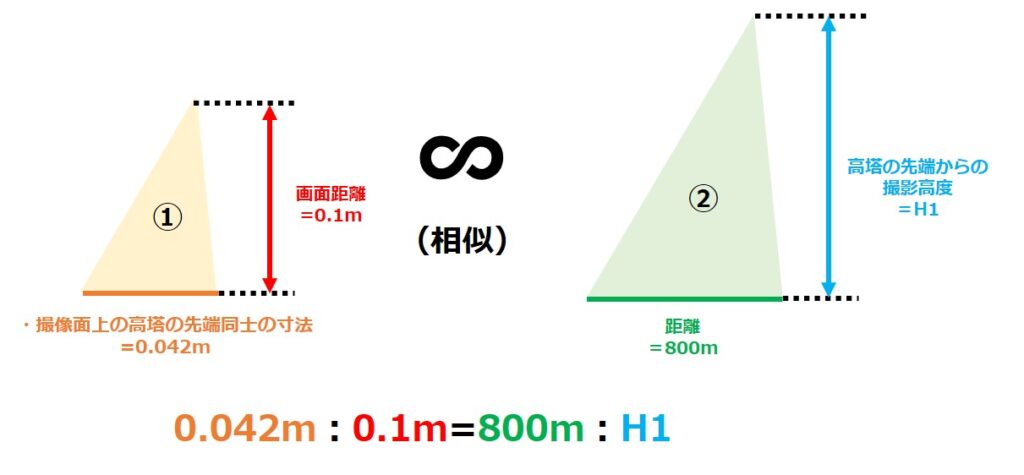
下図をよく見てみると、色を付けた三角形①と②が相似の関係であることが分かりますね。
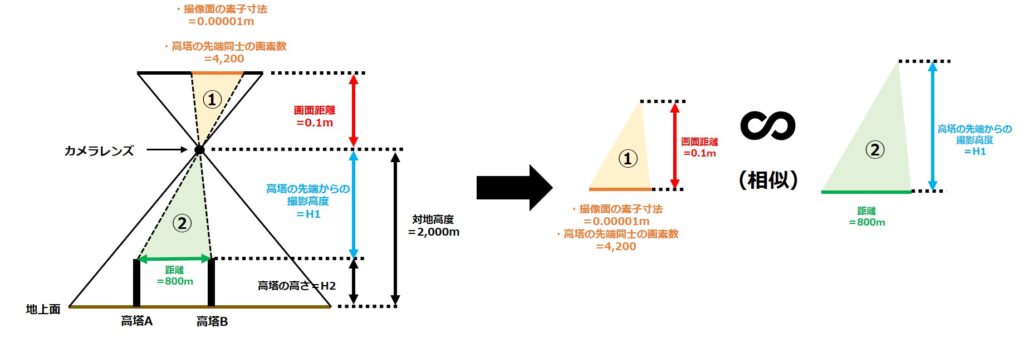相似の三角形同士の対応する辺と高さの比は同じになるので、比を利用した計算をすれば高塔の先端からの撮影高度（＝H1）を求めることができます。
ただ、三角形①の底辺の長さがわかっていませんので、まずは求めていきましょう。
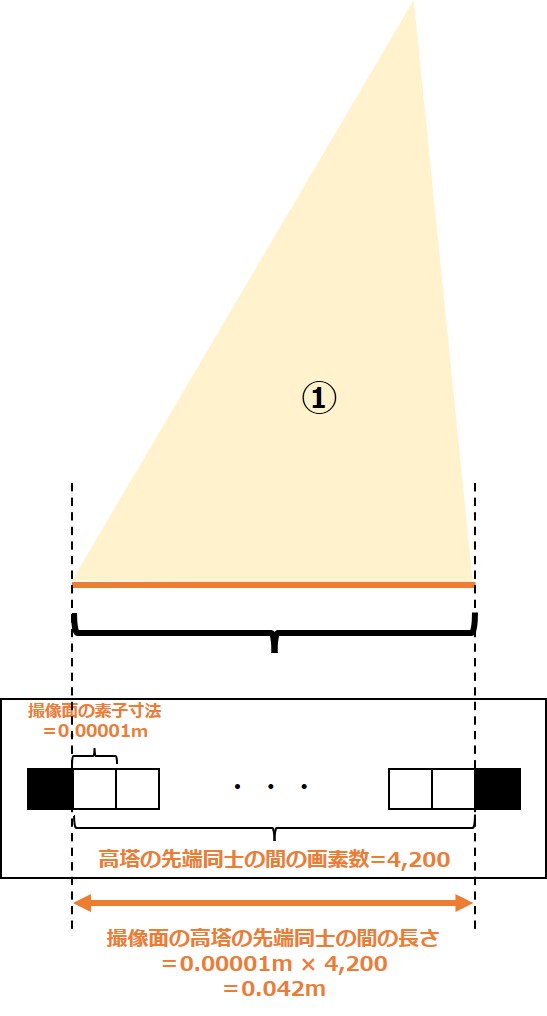
高塔の先端同士の間の画素数が4,200であり、その画素の寸法が0.00001であることがわかっているので「寸法×画素数」で撮像面の長さ（＝三角形①の底辺）がわかります。
下図のようなイメージですね。
よって
上図のような関係性になるので、
0.042m：0.1m＝800m：H1
⇔0.042m×H1＝0.1m×800m
⇔H1＝（0.1m×800m）/ 0.042m
⇔H1＝1904.7619…≒1905m
となります。
よって高塔の先端からの撮影高度H1＝1905mとなります。
手順３ 高塔の高さを求める
手順２で高塔の先端からの撮影高度を求めることができたので、図に盛り込むと以下のようになります。
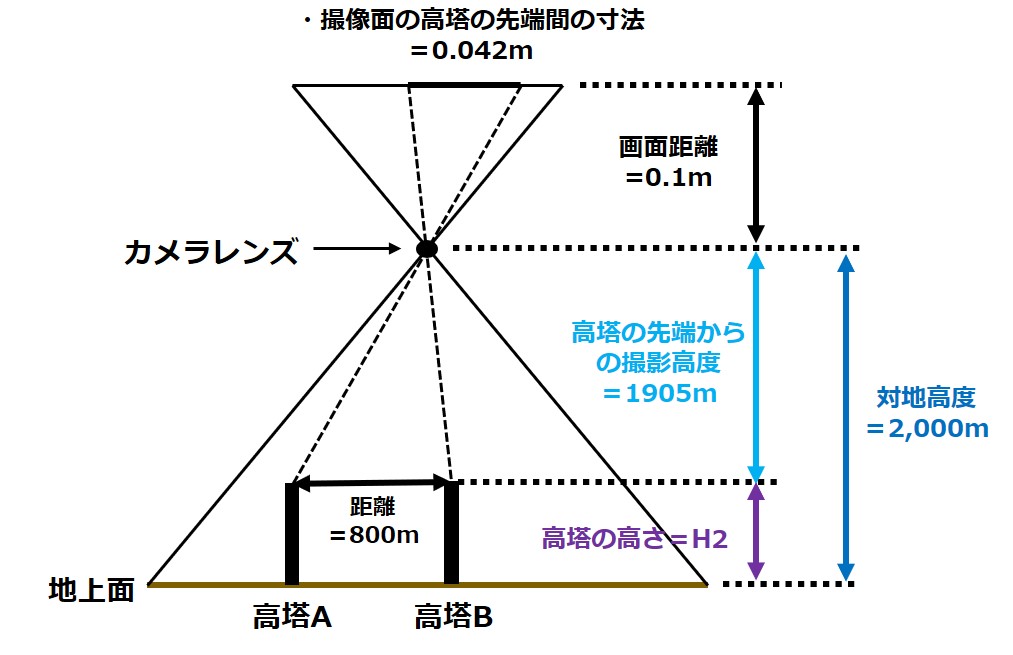図を見てみると、対地高度2,000mから高塔の先端からの撮影高度1905mをひけば、高塔の高さ（＝H2）を求められそうですね。
よって
H2＝2,000m－1905m
＝95m
となりますので、高塔の高さ＝95mと求めることができました。
この答えに対応する選択肢は「５」ということになります。
令和３年測量士補試験No.１９のまとめ
「写真測量」からの出題でした。
写真に写っている地物から高さを求める問題は比較的出題頻度が高めです。
三角形の相似を使えば解けますので、まずは図を書くことを習得する意識をもって取り掛かりましょう！
その他の測量士補試験の問題に挑戦！
令和3年のNO.19の問題を確認したら、その他の問題にも挑戦していきましょう！
本ブログでは各問題の解説を年度ごとに一覧にまとめたページがありますので、ぜひその記事からその他の問題に挑戦してみてください！
問題解説のまとめ記事はコチラからどうぞ！→過去問に挑戦！現役測量士の解説を読んで測量士補試験を攻略しよう！
さいごに
本ブログを参考にしていただきありがとうございます。
内容に関して不明な点、ご質問、指摘事項、感想などございましたら、コメントやメールにてご連絡ください。
励みになるとともに、本ブログをよりたくさんの皆様に有益なものにできると考えています。
ぜひお待ちしております。
お問い合わせ先：surveyor_kenzo☆aol.com
※ご連絡の際は☆を@に変更してください。