必要な用語や手法に関する解説も一緒におこなっていきますので、参考書代わりに本記事を使ってみてください!
目次
令和2年測量士補試験No.5の問題文
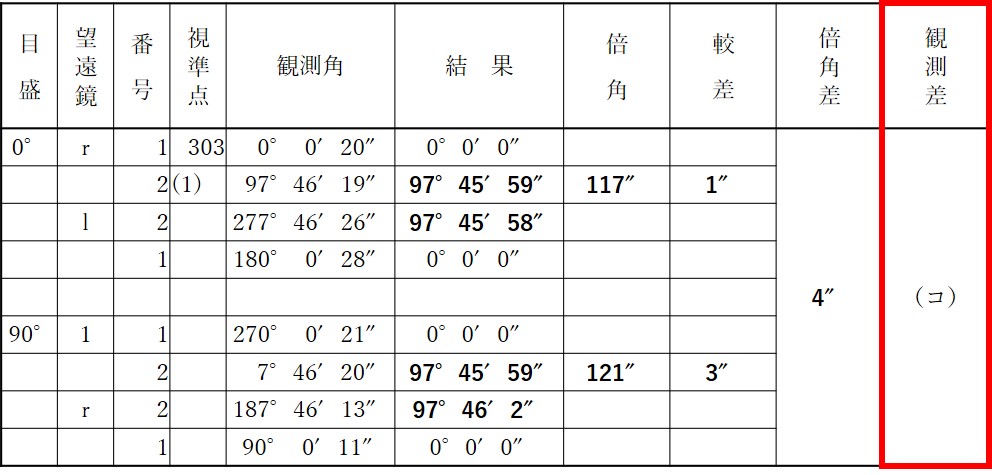
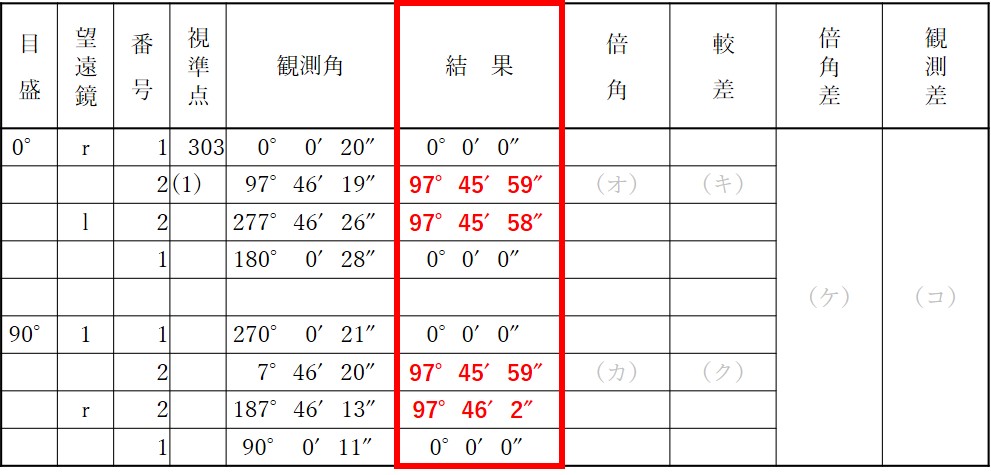
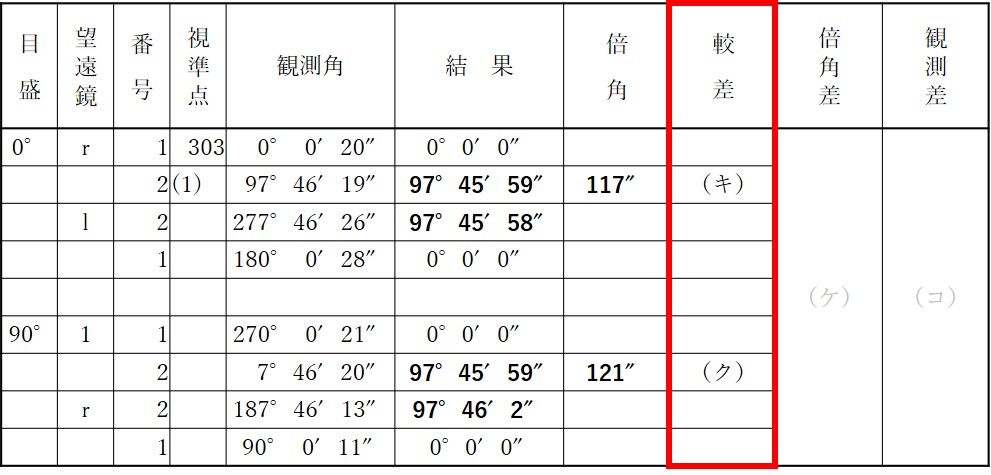
公共測量における 1 級基準点測量において,トータルステーションを用いて水平角を観測し,表 5 の観測角を得た。 ア ~ コ に入る数値のうち明らかに間違っているものはどれか。次の中から選べ。
- 結果のアは97°45′59″であり,イは97°45′58″である。
- 結果のウは97°45′59″であり,エは97°46′ 2″である。
- 倍角のオは117″であり,カは121″である。
- 較差のキは+ 1″であり,クは- 3″である。
- 倍角差のケは 4″であり,観測差のコは 2″である。
(令和2年測量士補試験問題集 No.5)
令和2年測量士補試験No.5の解答・解説
「多角測量」の分野からの出題です。
解答は「4」です。以下、表5の空欄を埋めるための各計算の解説です。
(ア)~(エ)観測結果の計算
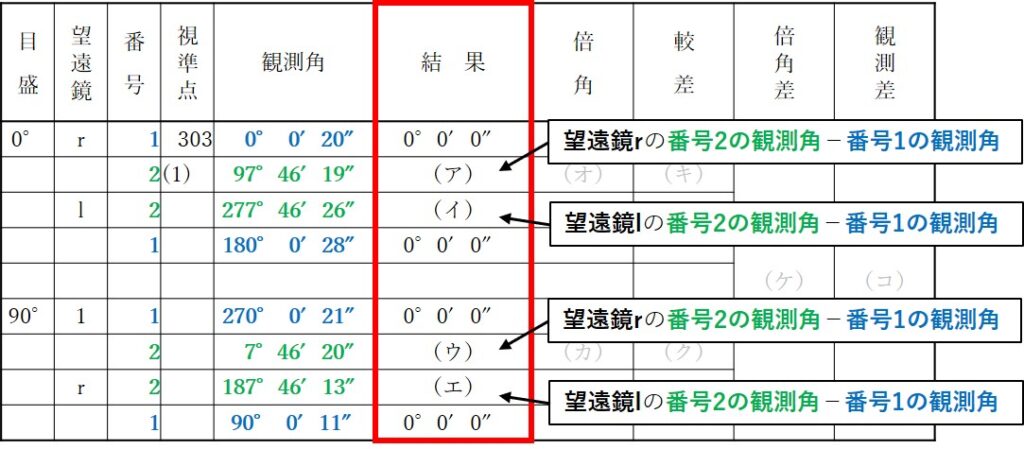
まずは(ア)~(エ)の空欄が該当する、観測結果についての計算です。
観測結果の値は、次のように計算していきます。
よって(ア)~(エ)はそれぞれ次のような計算式が成り立ちます。
あとはそれぞれ計算していけばよいのですが、(ウ)のように番号2の観測角より番号1の観測角の方が大きい値の場合は注意が必要です。
このまま計算すると答えが-(マイナス)になってしまうので、360°を足すというひと手間を加えます。
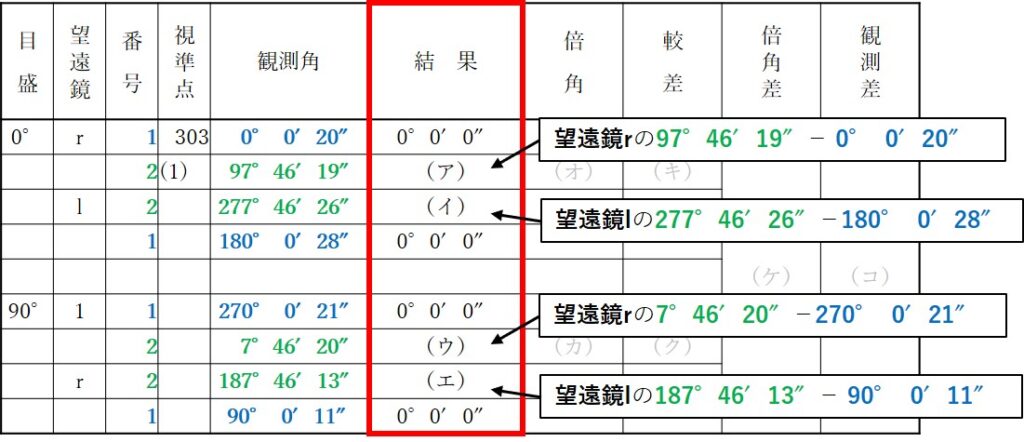
よってそれぞれの計算結果は
(ア)
97°46′19″- 0° 0′20″
=97°45′59″
(イ)
277°46′26″-180° 0′28″
=97°45′58″
(ウ)
7°46′20″-270° 0′21″+360°0′0″
=97°45′59″
(エ)
187°46′13″- 90° 0′11″
=97°46′2″
となります。
よってまとめると
(ア)97°45′59″
(イ)97°45′58″
(ウ)97°45′59″
(エ)97°46′2″
です。
(オ)(カ)倍角の計算
(オ)と(カ)では倍角の計算を行います。
対回と正反の観測とは
倍角の計算を行う上で倍角が何かを理解する必要があるのですが、そのためには「対回(ついかい)」と「正負の観測」を理解していないといけません。
「対回」とは一か所の角度を測る際の「正の観測」と「負の観測」のセットのこと。
「正の観測」とは左から右(時計回り)に向かって角度を測ること、「反の観測」とは右から左(反時計回りに)向かって角度を測ることです。
正の観測と反の観測をそれぞれ行い、その工程を一対回とします。
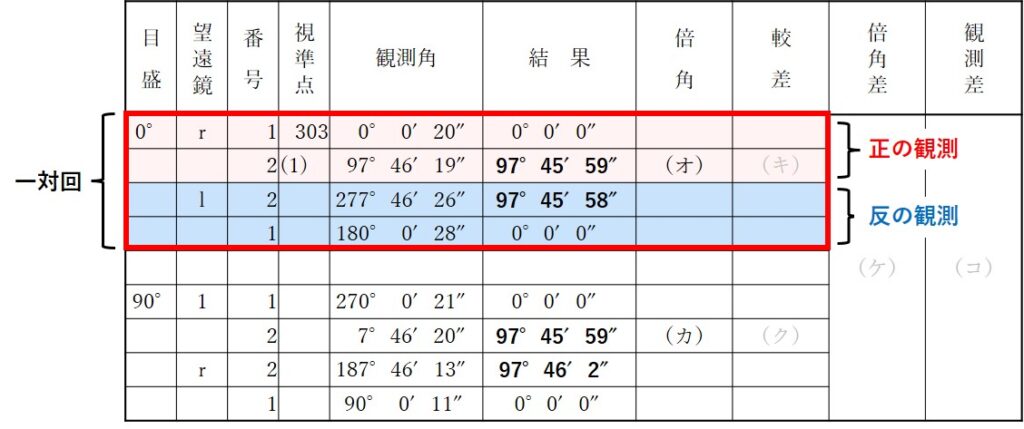
今回の問題の表5で言えば、対回とは2行目~5行目までのことで、望遠鏡rで得た観測結果(ア)が正の観測結果、望遠鏡lで得た観測結果(イ)が反の観測結果です。
また、一回目の対回のことを一対回、二回目の対回のことを二対回といったりします。
倍角とは
続いて、倍角について簡単におさえましょう!
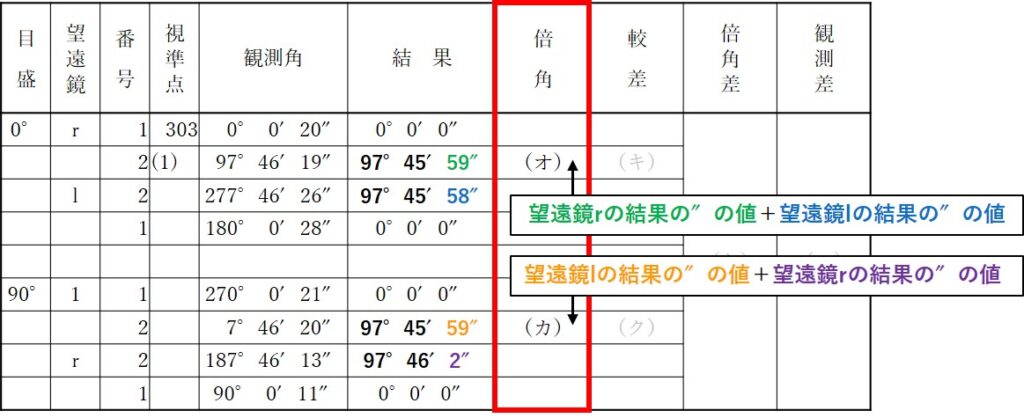
倍角とは「一対回の正の観測結果と反の観測結果の″(秒)の値を足した数値」のことを言います。
あくまで「″の値」のみなので、間違えないようにしましょう!
上の表の「2~5行目まで」と「下から4行目まで」がそれぞれ一対回のセットです。
以上のことをふまえた上で、倍角の計算を行っていきましょう!
倍角の計算
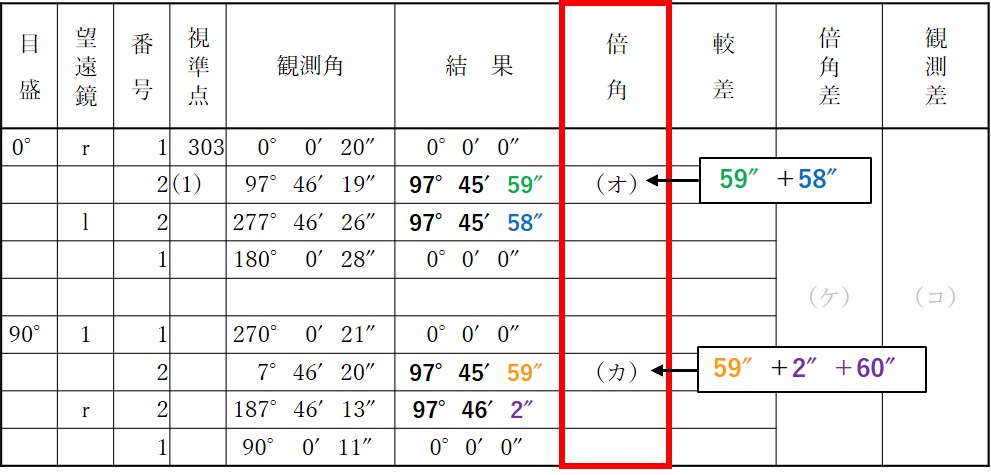
今回は、下の画像のように計算すると(オ)と(カ)それぞれの倍角の値が出ます。
ここで注意したいのが、下から2行目の「2″」の値です。
他の3つの値は45′〇″となっていますが、下から2行目だけは46′2″となってしまっています。
このままでは単位が合っていないので「1′=60″」であることをふまえて46′2″を45′62″と変換しなければなりません。
よって(オ)と(カ)それぞれの倍角を計算すると
(オ)
59″+58″=117″
(カ)
59″+62″=121″
となります。
(オ)117″
(カ)121″
となります。
(キ)(ク)較差の計算
(キ)と(ク)では較差の計算を行います。ちなみに格差は「かくさ」もしくは「こうさ」と読みます。
較差とは
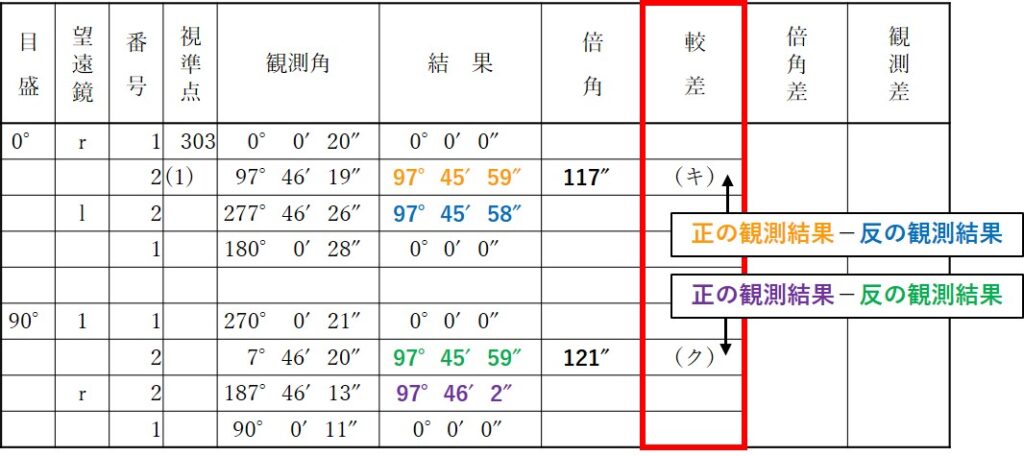
較差とは「一対回の中での観測結果の差」のことを指します。差を出すときは、
較差=(正の観測結果)-(反の観測結果)
で計算します。
ここで、注意が必要なのが二対回目(下から4行目まで)です。
二対回目の観測は反の観測からスタートします。引き算の順番には注意しましょう!
較差の計算
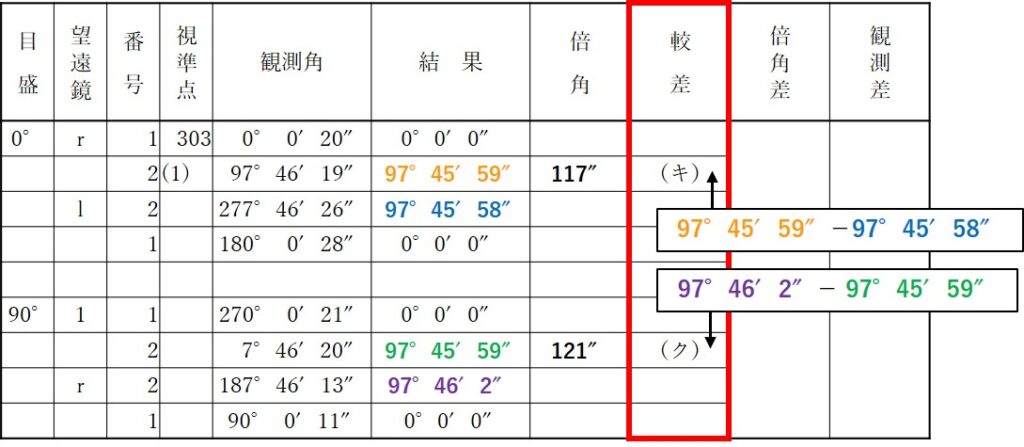
今回の問題では、較差は次のように計算します。
よって、(キ)と(ク)それぞれの較差を計算すると
(キ)
97°45′59″-97°45′58″=1″
(ク)
97°46′2″-97°45′59″=3″
となります。
よって
(キ)1″
(ク)3″
となります。
(ケ)倍角差の計算
(ケ)では倍角差の計算を行っていきます。
倍角差とは
倍角差とは名前の通り「倍角の差」のことです。
倍角は各対回の観測結果の秒を足した値であり、複数対回行っている場合は最も大きい倍角と最も小さい倍角の差を見ます。
倍角の差を確認することで観測結果の信頼性を確認することが目的です。
例えば、倍角差が大きい場合は成果の差が大きいということです。つまり、成果が間違っている可能性が高いと言えます。
一方で倍角差が小さい場合は成果の差が小さいということですので、安定して観測できていると言える根拠の1つになります。
今回の問題では2対回行っているので大きい倍角(2対回目)から小さい倍角(1対回目)をひくことで倍角差の値をわりだせますね。
倍角差の計算
前述したとおり、倍角差は大きい倍角(2対回目)から小さい倍角(1対回目)をひくことで導けます。
よって
倍角差(ケ)
121″-117″=4″
(ケ)4″
となります。
(コ)観測差の計算
(コ)では観測差を求めていきます。
観測差とは
観測差は「較差の差」のことを指します。
複数対回行っている場合は最も大きい較差と最も小さい較差の差を見ます。
較差=(正の観測結果)-(反の観測結果)なので各対回の較差の値が大きくても、その較差同士を比べたときに差が小さければその較差の値には器械そのものが持つ誤差が影響していると考えることができます。
言い換えると、器械そのものが持つ誤差が影響していて較差の値が出ているのであれば、正の観測か反の観測のどちらかに値が偏る、つまり+か-どちらかに偏ると言えます。
+と-どちらかに較差の値が偏っていれば、その差を計算しても値が小さくなるので、結果は安定していると判定できるわけです。
逆に、観測差(=較差の差)が大きければ、いずれかの対回の観測の結果が怪しいと言えます。
観測差の計算
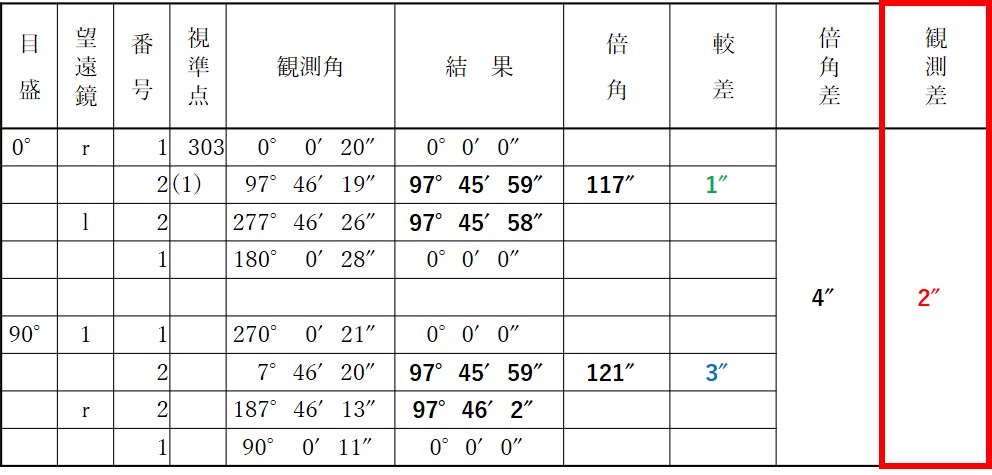
前述したとおり、観測差は「最も大きい較差-最も小さい較差」を計算して出します。
3″-1″=2″
(コ)2″
となります。
(ア)~(コ)のまとめと選択肢の比較
長々と計算の説明をしてきました。お疲れ様でした。
(ア)~(コ)までの値をまとめると次のようになります。
 あとは、上記表と選択肢の文章が合っているか比べていきましょう!
あとは、上記表と選択肢の文章が合っているか比べていきましょう!
それぞれの選択肢と比較
選択肢1「結果のアは97°45′59″であり,イは97°45′58″である。」
表の値と文章の値が一致しているので正しいです。
選択肢2「結果のウは97°45′59″であり,エは97°46′ 2″である。」
表の値と文章の値が一致しているので正しいです。
選択肢3「倍角のオは117″であり,カは121″である。」
表の値と文章の値が一致しているので正しいです。
選択肢4「較差のキは+ 1″であり,クは- 3″である。」
(キ)は表と文章で一致ていますが(ク)の値が一致していませんので間違いです。
2対回目の正の観測と反の観測の順番の違いの認識を間違えていると一致しません。
選択肢5「倍角差のケは 4″であり,観測差のコは 2″である。」
表の値と文章の値が一致しているので正しいです。
よって、本問の正解の選択肢は「4」であると言えます。
令和2年測量士補試験No.5のまとめ
「多角測量」の分野からの出題でした。
観測簿の記入は普段測量を行っていくうえでは欠かせない知識です。
今回の問題をしっかりとマスターして、実務に備えましょう!
計算が多めの印象だったかもしれませんが、慣れてくるとかなりすらすら計算できるようになってきます。
- 倍角
- 較差
- 倍角差
- 観測差
それぞれの語句の意味の理解とともに、反復して計算も器械的に解けるようにしていきましょう!
さいごに
さべろぐでは、測量士補試験合格を目指す人を応援しています!
受験に関する相談事や、内容に関して不明な点、ご質問、指摘事項、感想などございましたら、コメントやメールにてご連絡ください。
励みになるとともに、本ブログをよりたくさんの皆様に有益なものにできると考えています。
ぜひお待ちしております。
お問い合わせ先:surveyor_kenzo☆aol.com
※ご連絡の際は☆を@に変更してください。





と(ケ)の解答_.jpg)