必要な用語や手法に関する解説も一緒におこなっていきますので、参考書代わりに本記事を使ってみてください。
目次
令和3年測量士補試験No.6の問題文
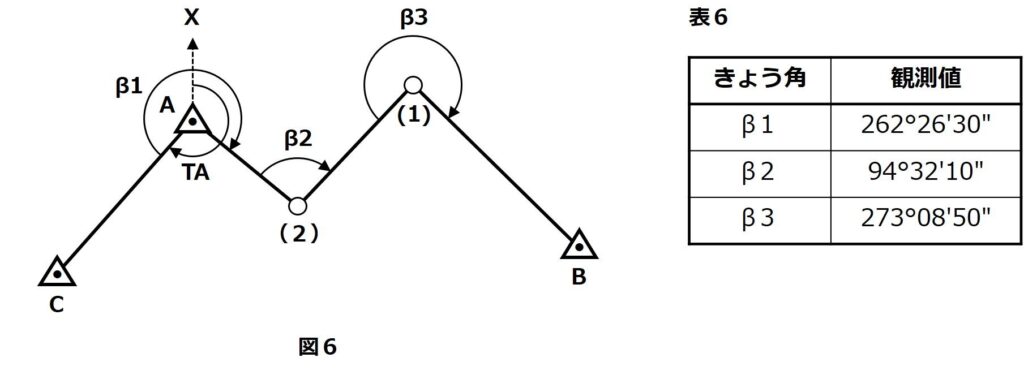
図6に示すように多角測量を実施し,表6のとおり,きょう角の観測値を得た。新点 ⑴ における既知点 B の方向角は幾らか。最も近いものを次の中から選べ。
ただし,既知点 A における既知点 C の方向角 TA は,225 ° 12 ′ 40 ″ とする。
なお,関数の値が必要な場合は,巻末の関数表を使用すること。(回答群)
1.42 ° 11 ′ 20 ″
2.44 ° 39 ′ 50 ″
3.86 ° 51 ′ 10 ″
4.135 ° 20 ′ 10 ″
5.137 ° 48 ′ 40 ″(令和3年測量士補試験問題集 No6より)
令和3年測量士補試験No.6の解答・解説
「多角測量」の分野からの出題になります。
解答は「4」となります。以下、詳しい計算手順の解説です。
方向角について理解する
まずは簡単に方向角について理解しましょう。
もう方向角は知ってます!という方はここは飛ばしてもらって大丈夫です!
それでは改めて方向角についてですが…
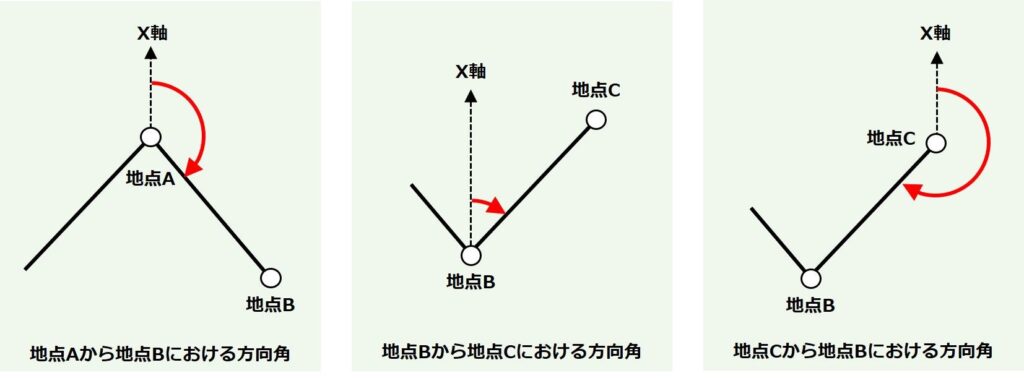
方向角とは「座標軸のうちX軸(縦軸)を起点として右回りに角度を測って、任意の直線にぶつかるまでの角度」を言います。
イメージとしては下図のようになります。
このイメージを理解していないと方向角の計算に対応できなくなってしまうため、必ず押さえておきましょう!
解答を得るまでの計算手順
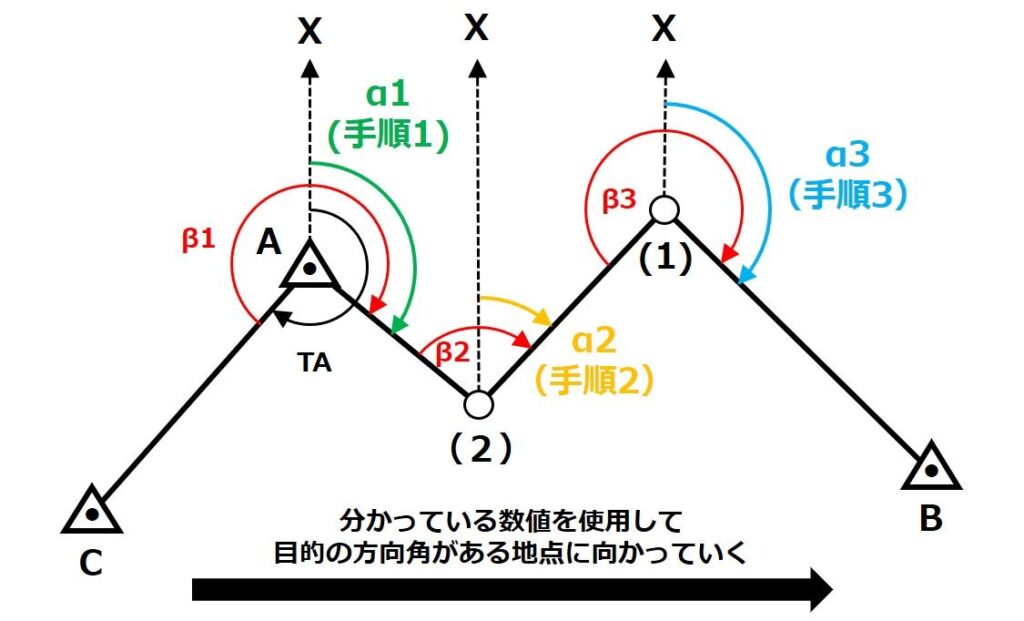
新点 ⑴ における既知点 B の方向角の値を得るためには、次の手順を踏む必要があります。
- 既知点Aにおける(2)の方向角(仮にα1とします)を求める
- (2)における(1)の方向角(仮にα2とします)を求める
- (1)における既知点Bの方向角(仮にα3とします)を求める
今回の問題では「既知点 A における既知点 C の方向角 TA は,225 ° 12 ′ 40 ″ 」と与えられているため、既知点Aから既知点に向かって順番に方向角を出していくのが良いですね。
それでは、それぞれの手順について詳しく見ていきます。
1.既知点Aにおける(2)の方向角(α1)を求める
まず、既知点Aに関する角度として以下の情報がわかっています。
- きょう角 β1=262°26′30″
- A →C の方向角 TA=225 ° 12 ′ 40 ″
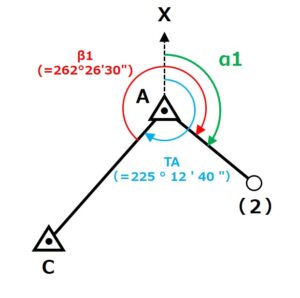
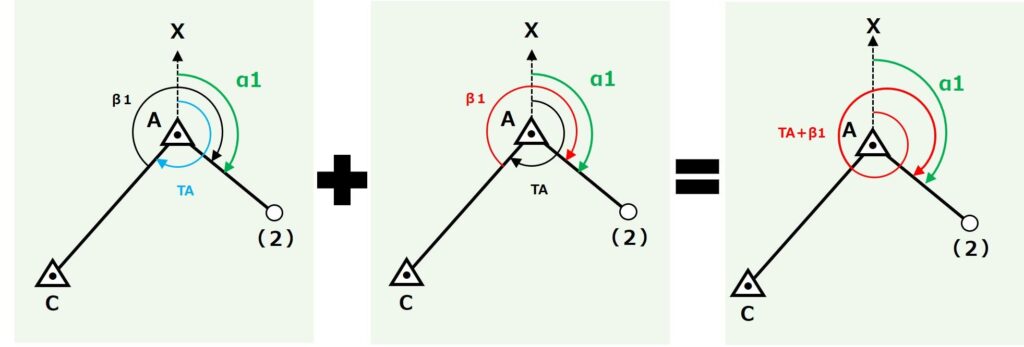
これらを図に表すとこのような形ですね。
ここで注目してほしいのが、TAとβ1の位置関係です。
TAの角度をX軸から追っていくと、β1の頭の部分(地点Aと地点Cを結んだ直線部分)にたどり着くのが分かりますか?
つまり、TAとβ1を足した角度はX軸から右回りにグルッと回って地点Aと地点(2)を結ぶ直線までの角度ということになります。
図で表すとこんな感じです。
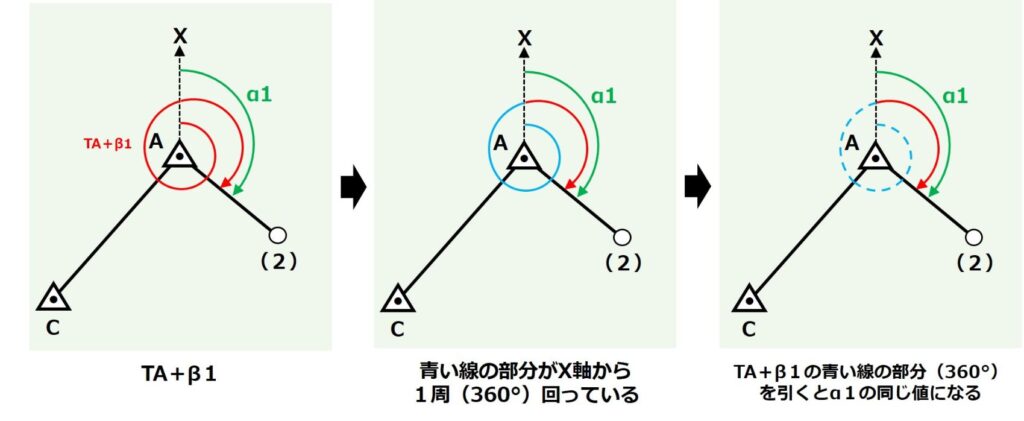
さらにここでTA+β1の角度を見てもらうと、1周回った部分(360°)を引けば求めたいα1の角度になりそうなこともわかります。
この流れを計算式に置き換えると次のようになります。
α1=TA+β1-360°
=225 ° 12 ′ 40 ″+262°26′30″-360°00′00″
=487°39′10″-360°00′00″
=127°39′10″
というわけで、既知点Aにおける(2)の方向角(α1)は127°39′10″となります。
2.(2)における(1)の方向角(α2)を求める
地点(2)に関する角度として以下のことがわかっています。
- きょう角 β2=94°32′10″
これだけではα2を出すことが難しいため、なんとか他の角度が出せないかどうかも考えてみます。
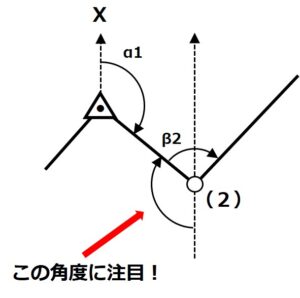
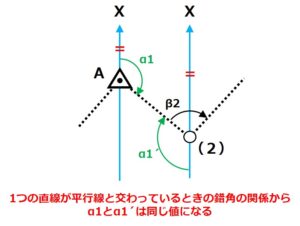
ここで「地点(2)の北軸」と「地点Aと地点(2)を結ぶ直線」の間の角度に注目してみましょう。
実はここの角度…手順1で出したα1と同じ値になるんです!
どういうことか、詳しく確認していきましょう。
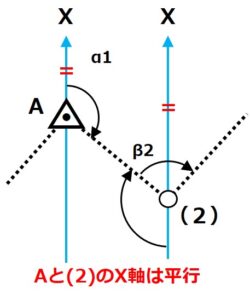
まず、方向角を考えるために地点Aと地点(2)にそれぞれX軸(縦軸)を設定しています。
この地点A・地点(2)それぞれのX軸は同じ方向を向いているため、平行の関係にあるんですね。
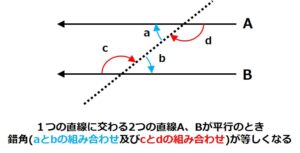
ここで中学校で習った「平行線と交わる直線のなす錯角は等しい」という関係を思い出してみましょう。
この関係から「地点(2)の北軸」と「地点Aと地点(2)を結ぶ直線」の間の角度(α1´とします)とα1は同じ値になることがわかります。
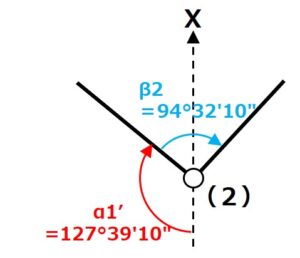
これで地点(2)に関する角度の数値が
- α1´=α1=127°39′10″
- β2=94°32′10″
と出ました。
ここからは基本的に手順1と考え方は同じです。
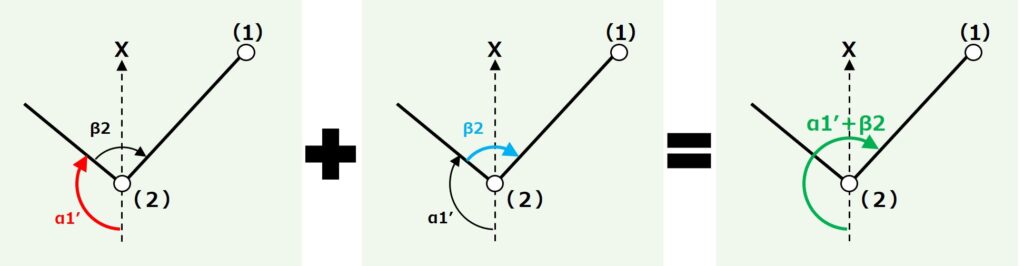
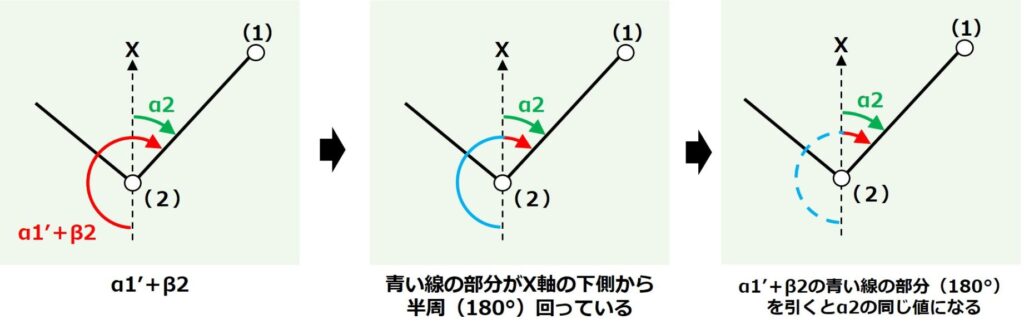
まず、α1'とβ2の位置関係からα1´とβ1を足した角度は「X軸の下側からぐるっと右回りに地点(2)と地点(1)を結ぶ直線までの角度」になることがわかります。
図で表すとこんな感じです。
さらにα1´にβ2を足した角度から半周分の角度(180°)を引いたら、求めたい「(2)における(1)の方向角(α2)」になりそうですね。
これらを式で表すと次のようになります。
α2=α1'+β2-180°00′00″
=127°39′10″+94°32′10″-180°00′00″
=222°11′20″-180°00′00″
=42°11′20″
というわけで、(2)における(1)の方向角(α2)は42°11′20″となります。
3.(1)における既知点Bの方向角(α3)を求める
基本的な考え方は手順2と全く同じです。
まず、問題文から与えられている地点(1)における角度の情報は
- きょう角 β3=273°08′50″
です。
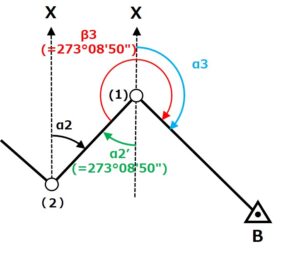
そして地点(2)と地点(1)のそれぞれのX軸が平行であることから、地点(1)のX軸の下側から(2)と(1)を結ぶ直線までの角度はα2と同じ角度になります。
本記事では地点(1)のX軸の下側から(2)と(1)を結ぶ直線までの角度をα2'とします。つまり
- α2=α2'=42°11′20″
となります。
以上のことを図で表すとこんな感じですね。
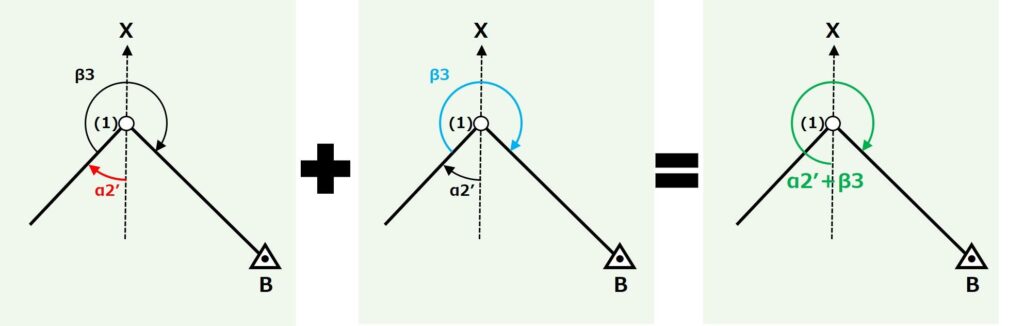
この図を見てみると、「α2'とβ3を足し角度」は「地点(1)のX軸の下側から地点(1)と地点Bを結ぶ直線までの角度」と同じになることがわかります。
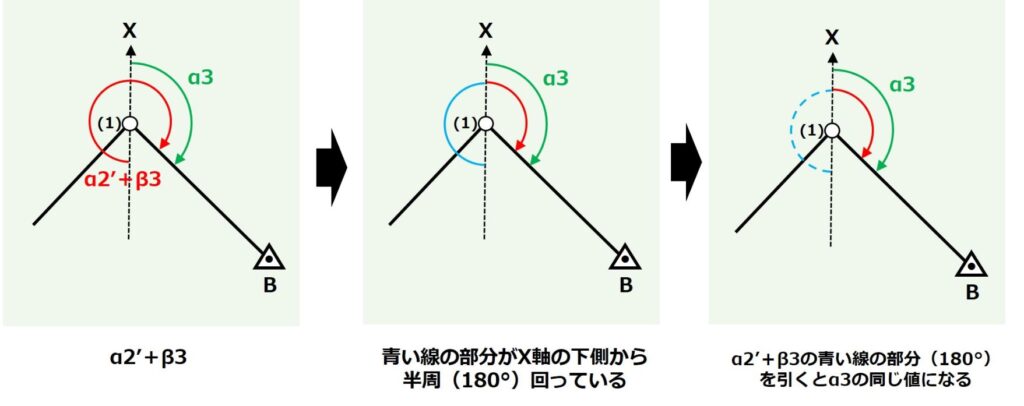
さらにα2´にβ3を足した角度から半周分の角度(180°)を引いたら、求めたい「(1)における既知点Bの方向角(α3)」です。
これらを式で表すとこんな感じです。
α3=α2'+β3-180°00′00″
=42°11′20″+273°08′50″-180°00′00″
=315°20′10″-180°00′00″
=135°20′10″
よって、(1)における既知点Bの方向角(α3)の角度は135°20′10″となります。
α3が今回の問題で出したかった解答なので135°20′10″にあてはまる選択肢は「4」となります。
令和3年測量士補試験No.6のまとめ
「多角測量」からの出題でした。
方向角を出す問題は出題頻度が高めなので必ず押さえる必要があります。
計算手順が多いように感じたかもしれませんが、やることは同じことの繰り返しです。
一度やり方を覚えれば、そこまで苦戦することもなくなります。
ぜひ、このパターンをおさえて貴重な得点源の1つにしちゃいましょう!
その他の測量士補試験の問題に挑戦!
令和3年のNO.6の問題を確認したら、その他の問題にも挑戦していきましょう!
本ブログでは各問題の解説を年度ごとに一覧にまとめたページがありますので、ぜひその記事からその他の問題に挑戦してみてください!
問題解説のまとめ記事はコチラからどうぞ!→過去問に挑戦!現役測量士の解説を読んで測量士補試験を攻略しよう!
さいごに
本ブログを参考にしていただきありがとうございます。
内容に関して不明な点、ご質問、指摘事項、感想などございましたら、コメントやメールにてご連絡ください。
励みになるとともに、本ブログをよりたくさんの皆様に有益なものにできると考えています。
ぜひお待ちしております。
お問い合わせ先:surveyor_kenzo☆aol.com
※ご連絡の際は☆を@に変更してください。